Theory

For a fixed-spread acquisition, the phase-encoded multisource data (i.e. supergathers) can be represented as

$$\textbf{d}=\sum_{i=1}^{S}\textbf{P}_{i}\textbf{d}_{i},$$ (1)

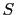where $S$ is the number of multiple shots and matrix 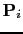$\textbf{P}_{i}$ represents the phase-encoding functions (in this study, the encoding functions involve random source time delay). All the 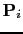$\textbf{P}_{i}$ are chosen to be unitary so that $\textbf{P}^{T}_{i}\textbf{P}_{i}$ is equal to the identity matrix.

In equation , I define $\textbf{d}$ as a supergather, which is the summation of shot gathers, each with shot excitation time shifted by a random time shift with a standard deviation greater than the source period. It is shown in Schuster et al. (2011) that the combination of random polarity changes, random time shifts and random shot locations is more effective at reducing crosstalk noise than the use of any of the three encoding functions alone. 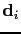I assume that the i-th CSG $\textbf{d}_{i}$ and the reflectivity model 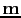$\textbf{m}$ are related by

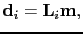$$\textbf{d}_{i}=\textbf{L}_{i}\textbf{m},$$ (2)

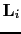where $\textbf{L}_{i}$ is the linear forward modeling operator associated with the i-th shot. This operator can represent either a Kirchhoff or a wave-equation modeling method (Mulder and Plessix, 2004). Plugging equation into , I get

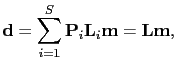$$\textbf{d}=\sum_{i=1}^{S}\textbf{P}_{i}\textbf{L}_{i}\textbf{m}=\textbf{Lm},$$ (3)

where the supergather modeling operator is defined as

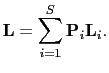$$\textbf{L}=\sum_{i=1}^{S}\textbf{P}_{i}\textbf{L}_{i}.$$ (4)