



Next: Numerical Results
Up: Least-squares Wave-equation Migration
Previous: Introduction
Contents
The theory for generalized diffraction-stack migration (GDM) was described by
Schuster (2002), who reformulated
the equations of RTM so that they can be reinterpreted as a GDM algorithm,
 |
|
|
(17) |
with the migration kernel defined as
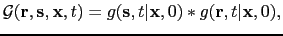 |
|
|
(18) |
where 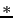 denotes temporal convolution and
denotes temporal convolution and 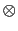 , together with
, together with 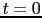 , represents the correlation at
zero-lag time (which is equivalent to a dot product in the data coordinates).
The
, represents the correlation at
zero-lag time (which is equivalent to a dot product in the data coordinates).
The
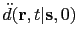 term represents
the second time derivative of the trace at the receiver point
term represents
the second time derivative of the trace at the receiver point 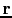 with the source point at
with the source point at  ,
while the
,
while the
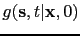 and
and
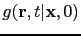 terms represent
the scattered Green's functions which, respectively, propagate the energy from the
subsurface trial image point
terms represent
the scattered Green's functions which, respectively, propagate the energy from the
subsurface trial image point 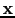 to the
surface source point at
to the
surface source point at  and
the receiver point
and
the receiver point 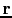 .
The term
.
The term
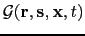 acts as the migration operator or focusing kernel
(Schuster, 2002)
which migrates the reflection in
acts as the migration operator or focusing kernel
(Schuster, 2002)
which migrates the reflection in
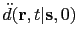 to the trial image point
to the trial image point 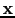 .
It is obtained by a FD solution to the wave equation with a point source
.
It is obtained by a FD solution to the wave equation with a point source  on
the surface and a scattering point at the image point
on
the surface and a scattering point at the image point 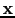 , and convolving this source-side Green's function
, and convolving this source-side Green's function
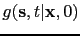 with the receiver-side Green's function
with the receiver-side Green's function
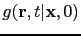 .
.
Figure:
Diffraction-stack migration versus generalized diffraction-stack migration.
a) Simple diffraction-stack migration operator (dashed hyperbola) and data, which only contains first arrival scattering
information. b) Generalized diffraction-stack migration operator (dashed hyperbolas) which contains all events in the
migration model, including multiples, diffractions and reflections.
|
|
A simple diagram shown in Figure ![[*]](crossref.png) illustrates the difference between the diffraction-stack
migration and GDM operators plotted in data-space coordinates.
Figure
illustrates the difference between the diffraction-stack
migration and GDM operators plotted in data-space coordinates.
Figure ![[*]](crossref.png) a shows the traditional migration curve
for diffraction-stack migration which is also known as Kirchhoff migration. The usual interpretation is that
the migration image at
a shows the traditional migration curve
for diffraction-stack migration which is also known as Kirchhoff migration. The usual interpretation is that
the migration image at 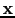 is given by summing the trace amplitudes along the hyperbola, i.e., the migration
image is the dot product of the recorded shot gathers with the migration operator
(a single hyperbolic curve shown in Figure
is given by summing the trace amplitudes along the hyperbola, i.e., the migration
image is the dot product of the recorded shot gathers with the migration operator
(a single hyperbolic curve shown in Figure ![[*]](crossref.png) a). Figure
a). Figure ![[*]](crossref.png) b illustrates the idea
behind GDM:
take the dot product of the recorded shot gathers with the generalized migration operator
b illustrates the idea
behind GDM:
take the dot product of the recorded shot gathers with the generalized migration operator
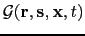 .
Note that all events are included in the generalized migration operator such as direct waves, multiples, reflections
and diffractions as well.
.
Note that all events are included in the generalized migration operator such as direct waves, multiples, reflections
and diffractions as well.
But the major problem with the above approach is that the migration operator
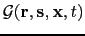 is a
five-dimensional matrix with the dimension size determined by the model size,
the number of sources and receivers, and the number of samples within a trace.
It means that
is a
five-dimensional matrix with the dimension size determined by the model size,
the number of sources and receivers, and the number of samples within a trace.
It means that
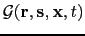 is too expensive to be stored.
To reduce the the cost of I/O and storage of the
is too expensive to be stored.
To reduce the the cost of I/O and storage of the
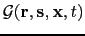 ,
I only store the early-arrivals of
,
I only store the early-arrivals of
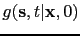 followed by skeletonization
to reduce the size of the migration kernel by at least two orders-of-magnitude.
followed by skeletonization
to reduce the size of the migration kernel by at least two orders-of-magnitude.
The skeletonized least-squares GDM algorithm is as follows:
- Compute the Green's functions
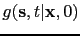 by a numerical solution to the wave equation
for a point source at trial image point
by a numerical solution to the wave equation
for a point source at trial image point 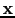 and recorded at source position
and recorded at source position  .
Since
.
Since  occupies the same positions as
occupies the same positions as 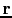 , then
, then
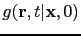 is considered the same as
is considered the same as
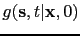 .
.
- Skeletonize
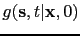 to
to
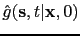 . Early-arrivals
are used and each
important early-arrival event is replaced by a single time sample after skeletonization.
In this way, a calculated Green's function trace
with 501 samples is reduced to a sparse trace with about 25 samples.
. Early-arrivals
are used and each
important early-arrival event is replaced by a single time sample after skeletonization.
In this way, a calculated Green's function trace
with 501 samples is reduced to a sparse trace with about 25 samples.
- The skeletonized Green's function
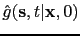 is associated with the
recording position at
is associated with the
recording position at  and
and
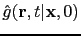 is that recorded at
is that recorded at 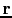 .
Those two Green's functions are convolved to generate the migration kernel:
.
Those two Green's functions are convolved to generate the migration kernel:
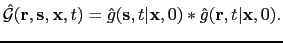 |
|
|
(19) |
- The migration operator
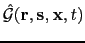 is a
Kirchhoff-like kernel
that describes, for a single shot gather, pseudo-hyperbolas of multiarrivals in
is a
Kirchhoff-like kernel
that describes, for a single shot gather, pseudo-hyperbolas of multiarrivals in
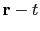 space.
The reflection energy in a recorded shot gather
space.
The reflection energy in a recorded shot gather
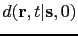 is then summed along such
pseudo-hyperbolas to give the migration image,
is then summed along such
pseudo-hyperbolas to give the migration image,
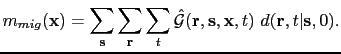 |
|
|
(20) |
- The above
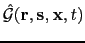 is used for iterative LSM
by a conjugate gradient method.
is used for iterative LSM
by a conjugate gradient method.
The advantages of skeletonized least-squares GDM are that
1). the high-frequency approximation of Kirchhoff migration is largely not needed;
2). the storage requirement for the migration kernel is reduced by more than two orders-of-magnitude
compared to storing every sample in a calculated migration kernel;
3). these migration operators do not need to be recalculated for each LSM iteration;
4). inclusion of just a few important early-arrival events can significantly reduce
artifacts seen in conventional RTM images.
In contrast, the main drawback of skeletonized least-squares GDM is that the choice of important events is
somewhat arbitrary and so can lead to missing important information in the migration operator. However,
the migration operator is only as accurate as our knowledge of the subsurface velocity model so
important events might be just the early-arrivals.




Next: Numerical Results
Up: Least-squares Wave-equation Migration
Previous: Introduction
Contents
Ge Zhan
2013-07-08

![[*]](crossref.png) illustrates the difference between the diffraction-stack
migration and GDM operators plotted in data-space coordinates.
Figure
illustrates the difference between the diffraction-stack
migration and GDM operators plotted in data-space coordinates.
Figure ![[*]](crossref.png) a shows the traditional migration curve
for diffraction-stack migration which is also known as Kirchhoff migration. The usual interpretation is that
the migration image at
a shows the traditional migration curve
for diffraction-stack migration which is also known as Kirchhoff migration. The usual interpretation is that
the migration image at ![]() is given by summing the trace amplitudes along the hyperbola, i.e., the migration
image is the dot product of the recorded shot gathers with the migration operator
(a single hyperbolic curve shown in Figure
is given by summing the trace amplitudes along the hyperbola, i.e., the migration
image is the dot product of the recorded shot gathers with the migration operator
(a single hyperbolic curve shown in Figure ![[*]](crossref.png) a). Figure
a). Figure ![[*]](crossref.png) b illustrates the idea
behind GDM:
take the dot product of the recorded shot gathers with the generalized migration operator
b illustrates the idea
behind GDM:
take the dot product of the recorded shot gathers with the generalized migration operator
![]() .
Note that all events are included in the generalized migration operator such as direct waves, multiples, reflections
and diffractions as well.
.
Note that all events are included in the generalized migration operator such as direct waves, multiples, reflections
and diffractions as well.
![]() is a
five-dimensional matrix with the dimension size determined by the model size,
the number of sources and receivers, and the number of samples within a trace.
It means that
is a
five-dimensional matrix with the dimension size determined by the model size,
the number of sources and receivers, and the number of samples within a trace.
It means that
![]() is too expensive to be stored.
To reduce the the cost of I/O and storage of the
is too expensive to be stored.
To reduce the the cost of I/O and storage of the
![]() ,
I only store the early-arrivals of
,
I only store the early-arrivals of
![]() followed by skeletonization
to reduce the size of the migration kernel by at least two orders-of-magnitude.
followed by skeletonization
to reduce the size of the migration kernel by at least two orders-of-magnitude.