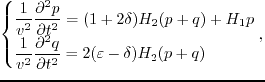Equations

Following Alkhalifah's (2000) work, Zhou et al. (2006b) formulated the 2D TTI acoustic wave propagation as a coupled 2nd-order PDE system. The 3D TTI equations are based on two 3D rotations, which is an extension to the 3D VTI and 2D TTI equations of Zhou et al. The 3D version is expressed as (Zhang and Zhang, 2008; Fletcher et al., 2008)

$$\left\{ \begin{array}{ll} \displaystyle\frac{1}{v^2} \displayst... ...}{\partial t^2} = 2(\varepsilon-\delta)H_2( p + q ) \\ \end{array} \right. ,$$ (21)

where differential operators $H_1$ and $H_2$ are given by

$$\left\{ \begin{array}{ll} H_1 = \bigg[ \sin{\theta}\cos{\phi} \... ...\partial^2_x + \partial^2_y + \partial^2_z \bigg) - H_1 \end{array} \right. .$$ (22)

In the above coupled equations, $p$ is the usual pressure wavefield, $q$ is an introduced auxiliary wavefield to ease numerical computations. Five model cubes are required in the case of TTI: one P-wave velocity model $v$ to describe the wave propagation along the symmetry axis, two dimensionless parameters $\varepsilon$ and $\delta$ (Thomsen, 1986) to characterize the anisotropy, and two angles $\theta$ (dip measured to the vertical) and $\phi$ (azimuth) to define the symmetry direction.

In my algorithm, the TTI coupled equations are solved with a hybrid FD and PS method, carrying out the space-derivative calculation in the wavenumber domain and the time stepping by an explicit FD method. To speed up the computation in areas of higher velocity values, the PS scheme is replaced by the FD method to compute the Laplacian operator for saving computational costs.