


Next: TTI decoupled equations
Up: Decoupled Equations in TI
Previous: Decoupled Equations in TI
Contents
Pestana et al. (2011) started with the exact phase velocity expression for VTI media (Tsvankin, 1996)
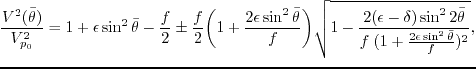 |
(31) |
where
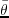 is the phase angle measured to the symmetry axis and
is the phase angle measured to the symmetry axis and
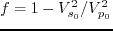 .
Here, the plus sign corresponds to the P wave and the minus sign corresponds to the SV wave.
.
Here, the plus sign corresponds to the P wave and the minus sign corresponds to the SV wave.
By revisiting equation 3.1 and expanding the square root to first order
(i.e.,
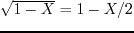 ),
Pestana et al. (2011) got the following approximations for the P wave and SV wave phase velocities
),
Pestana et al. (2011) got the following approximations for the P wave and SV wave phase velocities
 |
(32) |
Equations 3.2 are good approximations for the P wave and SV wave
dispersion relations when
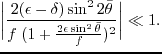 |
(33) |
Since we have the following relations
 and
and
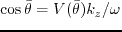 with
with
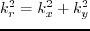 ,
where
,
where 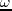 is the angular frequency,
is the angular frequency,
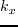 ,
, 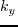 and
and 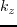 are spatial wavenumbers.
So I get
are spatial wavenumbers.
So I get
 .
Plugging them into equations 3.2 gives
.
Plugging them into equations 3.2 gives
![$\displaystyle \left\{ \begin{array}{ll} \omega^2=V^2_{p_0} \bigg[ (1+2\epsilon)...
...r k^2_z}{F k^2_r+k^2_z} \bigg] \;\;\;\;\;\mbox{(SV wave)} \end{array} \right. ,$](img56.png) |
(34) |
where
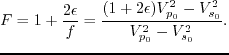 |
(35) |
Equations 3.4 are equivalent to the P8 and SV8 approximations in
the review paper of Fowler (2003).
Setting 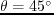 (i.e.,
(i.e.,
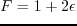 ), equations 3.4 reduce
to the dispersion relations used by Liu et al. (2009).
), equations 3.4 reduce
to the dispersion relations used by Liu et al. (2009).



Next: TTI decoupled equations
Up: Decoupled Equations in TI
Previous: Decoupled Equations in TI
Contents
Ge Zhan
2013-07-09
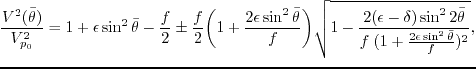
![]() ),
Pestana et al. (2011) got the following approximations for the P wave and SV wave phase velocities
),
Pestana et al. (2011) got the following approximations for the P wave and SV wave phase velocities
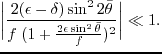
![]() and
and
![]() with
with
![]() ,
where
,
where ![]() is the angular frequency,
is the angular frequency,
![]() ,
, ![]() and
and ![]() are spatial wavenumbers.
So I get
are spatial wavenumbers.
So I get
![]() .
Plugging them into equations 3.2 gives
.
Plugging them into equations 3.2 gives