Discussion and Conclusion

In this chapter, I implemented a frequency-selection encoding strategy to speed up the least-squares reverse time migration of marine data. The traditional random phase encoding method is not applicable to marine data due to the mismatch in acquisition geometry between the observed data and the calculated synthetic data. With frequency-selection encoding, all the shots are encoded with encoding functions that are orthogonal to each other in the frequency domain, so the calculated synthetic data can be effectively decoded at the receiver locations for comparison with the observed data. Because of the data redundancy in the frequency domain, the frequency sampling rate can be large, which leads to significant computational savings. Numerical tests on part of the Marmousi2 model show that the frequency-selection encoding can significantly improve the efficiency of the LSRTM and reduce its cost to the level of conventional shot domain RTM. Empirical results suggest that the LSRTM with frequency-selection encoding is an efficient method to produce better images than conventional RTM.

Figure 3.1: The Marmousi2 model: (a) the modified Marmousi2 velocity model and (b) the smooth migration velocity.

Figure 3.2: A 20 Hz Ricker wavelet (a) and its associated frequency spectrum.

Figure 3.3: Harmonic simulation for a 25-Hz source at 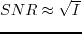$x=4km$ and recorded at 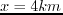$x=6km$ (a). Panel (b) plots the frequency spectrums of the first 8 secs (black) and second 8 secs (red) and panel (c) shows the zoom view of the part between 20-30 Hz.

Figure 3.4: Comparison of recorded traces with different simulation method. The black line indicates the recorded trace from time-domain simulation with a broadband wavelet; the red line is the stack of 400 harmonic traces (0-8 secs) and blue line (8-16 secs).

Figure 3.5: Ray diagrams for the reflections for the ocean bottom and the deepest reflector. The difference in arrival times of these two phases is used to estimate the necessary frequency sampling rate.

Figure 3.6: The true reflectivity of the Marmousi2 Model.

Figure 3.7: A common shot gather with shot location at 3 km offset.

Figure 3.8: Migration images obtained by (a) the conventional shot-domain RTM method and (b) the iterative stacking method.

Figure 3.9: The frequency-selection LSRTM image after (a) 1 iteration, (b) 20 iterations, and (c) 80 iterations.

Figure 3.10: Zoom view comparison of (a) shot-domain RTM image and (b) frequency-selection LSRTM image for the shallow part.

Figure 3.11: Zoom view comparison of (a) shot-domain RTM image and (b) frequency-selection LSRTM image for the deep part.

Figure 3.12: The migration velocity model for the field data.

Figure 3.13: A common shot gather with shot location at 11.3 km offset after preprocessing.

Figure 3.14: The migration images obtained with (a) the conventional RTM method and (b) the frequency-selection LSRTM method. Red and blue boxes indicate the area for zoom views.

Figure 3.15: Zoom view of the red box for (a) the conventional RTM image and (b) the frequency-selection LSRTM image.

Figure 3.16: Zoom view of the blue box for (a) the conventional RTM image and (b) the frequency-selection LSRTM image.