



Next: Conclusions
Up: Super-virtual Interferometric Diffractions as
Previous: Field Data Example
Contents
I presented the general theory
of super-virtual diffraction interferometry where the signal-to-noise ratio
(SNR) of
diffraction arrivals can
be theoretically increased by the factor 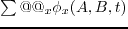 , where
, where 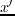 is the number of
receiver and source positions associated with the recording
of the diffractions.
There are two steps to this methodology: correlation and summation of the data
to generate traces with
virtual diffraction arrivals, followed by the convolution and stacking of the data
with the virtual traces to create super-virtual diffractions.
This method is valid for any
medium that generates diffraction arrivals due to isolated subwavelength scatterers.
There are at least three benefits with this methodology:
1). the diffraction arrivals can be used
as migration operators (Schuster, 2002; Brandsberg-Dahl et al., 2007; Sinha et al., 2009); 2). the diffraction arrivals
can be used for estimating source and receiver statics; 3). estimation of velocities by traveltime tomography or MVA.
is the number of
receiver and source positions associated with the recording
of the diffractions.
There are two steps to this methodology: correlation and summation of the data
to generate traces with
virtual diffraction arrivals, followed by the convolution and stacking of the data
with the virtual traces to create super-virtual diffractions.
This method is valid for any
medium that generates diffraction arrivals due to isolated subwavelength scatterers.
There are at least three benefits with this methodology:
1). the diffraction arrivals can be used
as migration operators (Schuster, 2002; Brandsberg-Dahl et al., 2007; Sinha et al., 2009); 2). the diffraction arrivals
can be used for estimating source and receiver statics; 3). estimation of velocities by traveltime tomography or MVA.
The problem with this method is that there will be artifacts associated with coherent events and quality degradation due to a limited recording aperture and a coarse spacing of the source and receivers.
Figure:
The steps for creating super-virtual diffraction arrivals.
(a) Correlation of the recorded trace at
with
that at
for a source at
to give the correlated trace
with
the virtual diffraction having traveltime
denoted by
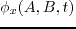 .
This arrival time will be the same for all source positions
.
This arrival time will be the same for all source positions 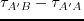 ,
so stacking
will enhance
the SNR of the virtual diffraction by
,
so stacking
will enhance
the SNR of the virtual diffraction by 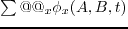 .
(b) Similar to that in (a) except the virtual diffraction traces
are convolved with the actual diffraction traces and stacked
for different
geophone positions
.
(b) Similar to that in (a) except the virtual diffraction traces
are convolved with the actual diffraction traces and stacked
for different
geophone positions  to give the (c) super-virtual trace with an
enhanced SNR. Here,
to give the (c) super-virtual trace with an
enhanced SNR. Here,  denotes the
number of coincident source and receiver positions.
denotes the
number of coincident source and receiver positions.
|
|
Figure 4.2:
(a) Geometry for computing virtual Green's functions
 from the recorded data
from the recorded data
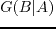 and
and
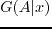 using the reciprocity
theorem of correlation type in an arbitrary acoustic medium of constant density.
(b) Geometry for computing super-virtual Green's functions
using the reciprocity
theorem of correlation type in an arbitrary acoustic medium of constant density.
(b) Geometry for computing super-virtual Green's functions
 from the recorded data
from the recorded data
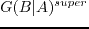 and the virtual data
and the virtual data
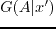 using the reciprocity theorem of convolution type.
using the reciprocity theorem of convolution type.
|
|
Figure 4.3:
Part of the BP2004 velocity model with three diffractors below the salt body.
|
|
Figure 4.4:
Synthetic data results for part of the BP2004 model. (a) A common shot gather with a source at offset 6 km. Red lines indicate the time window and the moveout of the diffraction event. (b) The diffraction event within a small time window. (c) The result after median filtering and (d) after processing the median filtered data to get the super-virtual diffraction.
|
|
Figure 4.5:
Velocity model with a fault and two diffractors.
|
|
Figure 4.6:
Synthetic data results for the fault model. (a) A common shot gather with a source at offset 36 m. Red lines indicate the time window of the diffraction event. (b) The diffraction event within a small time window. (c) The result after median filtering and (d) after processing the raw data to get the super-virtual diffraction.
|
|
Figure 4.7:
The super-virtual diffraction. In this figure, the red line indicates the predicted diffraction arrival times and the blue line indicates the picked arrival times.
|
|
Figure 4.8:
Friendswood cross-well data example. (a) A common shot gather with a source at depth of 36.6 m. Red lines indicate the time window and the moveout of the diffraction event. (b) The diffraction event within a small time window. (c) The result after median filtering and (d) the super-virtual diffraction.
|
|




Next: Conclusions
Up: Super-virtual Interferometric Diffractions as
Previous: Field Data Example
Contents
Wei Dai
2013-07-10