Lower Wavenumber Resolution with Prism Waves and Free-surface Multiples

To demonstrate the enhanced wavenumber coverage of multiples, the point-source response of the yellow vertical reflector in Figure 4.10 is computed by a finite-difference method. The trace is windowed about the reflections and then migrated by RTM to get the prism wavepath image (Dai and Schuster, 2013). As the length $L$ of the prism ray gets longer, the wavepath becomes thicker by $\sqrt{\lambda L}$ . 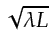In this way, the deep prism-reflection wavepath provides lower wavenumber information about the model compared to primaries. Such low wavenumbers are at the top of the FWI wish list for providing a good starting model for subsalt imaging.

Another example is shown in Figure 4.11. Here, the prism-wave reflection in b) achieves the same low-wavenumber resolution as the 1st-order free-surface multiple in a), but only requires about 1/2 the source-geophone offset of a). The deeper the reflector for the free-surface multiple, the thicker the wavepath and the lower the wavenumber in the estimated model.

Figure 4.11: Wavepaths for a) the 1st-order free-surface multiple and b) the prism-wave reflection from the yellow block. Note, the source-geophone offset for b) is about 1/2 that for a), and the dashed ellipse is the wavepath for the mirror source at the bottom left.