Prestack Split-Step Migration
Figure B.1:
Flowcharts for prestack split-step modeling and migration.
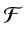 ,
,
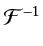 ,
,
 , and
, and
 denote
the Fourier transform, the inverse Fourier transform, the phase shift operator,
and the phase correction operator, respectively
(see text for details).
(a) The source wavefield
denote
the Fourier transform, the inverse Fourier transform, the phase shift operator,
and the phase correction operator, respectively
(see text for details).
(a) The source wavefield
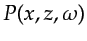 is propagated from the surface of the earth to
depth
is propagated from the surface of the earth to
depth 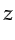 in steps
in steps 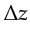 .
(b) At each depth
.
(b) At each depth 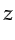 of the earth, a reflected wave is generated by
of the earth, a reflected wave is generated by
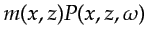 ,
where
,
where 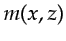 is a reflectivity model.
The wave is then propagated upward to the surface
is a reflectivity model.
The wave is then propagated upward to the surface 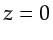 .
The total reflected wavefield
.
The total reflected wavefield
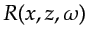 consists of the superposition of the reflected
and propagated waves originating from below.
The total reflected wavefield collected at the surface is the data, i.e.,
consists of the superposition of the reflected
and propagated waves originating from below.
The total reflected wavefield collected at the surface is the data, i.e.,
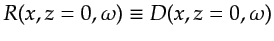 .
(c) The data are
then downward continued from the surface back to depth
.
(c) The data are
then downward continued from the surface back to depth 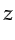 in steps
in steps 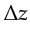 . Finally,
the migration image
. Finally,
the migration image 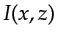 (not shown) is constructed by applying the imaging condition:
(not shown) is constructed by applying the imaging condition:
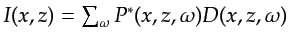 ,
or
,
or
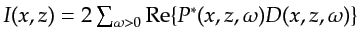 ,
assuming the DC component is 0.
,
assuming the DC component is 0.
|
![\includegraphics[width=3.35in]{fig/phaseShiftFlowchart}](img499.png) |
The steps of prestack split-step migration are described in the flowcharts shown in
Figure B.1. This presentation closely follows Kuehl and Sacchi (1999),
and is included here for convenience
because analysis of computational complexity refers to it.
Consider first the forward propagation of a wavefield.
The split-step operator
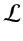 per layer can be decomposed into a succession
of four linear operators
per layer can be decomposed into a succession
of four linear operators
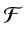 ,
,
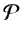 ,
,
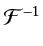 ,
and
,
and
 . First, the seismic wavefield
. First, the seismic wavefield
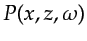 at
at 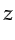 is
transformed to the wavenumber
is
transformed to the wavenumber 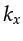 domain by the Fourier operator
domain by the Fourier operator
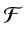 .
Second, the phase-shift operator
.
Second, the phase-shift operator
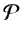 is applied to the wavefield in the
is applied to the wavefield in the
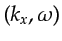 domain:
domain:
where 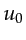 is the mean slowness for the current layer.
Third,
is the mean slowness for the current layer.
Third,
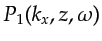 is transformed to the space
is transformed to the space 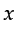 domain by the inverse
Fourier operator
domain by the inverse
Fourier operator
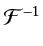 . Fourth, the phase correction operator
. Fourth, the phase correction operator
 is applied in the
is applied in the
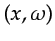 domain. This accounts for the lateral slowness variation
domain. This accounts for the lateral slowness variation
 :
:
 |
(7.2) |
Altogether, it is given that
of which the adjoint is
The adjoint operator
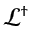 applies to the case of `backward propagation', or downward
continuation of the data, as illustrated in Figure B.1(c).
This ensures that the migration operator is the adjoint of the
forward modeling counterpart.
applies to the case of `backward propagation', or downward
continuation of the data, as illustrated in Figure B.1(c).
This ensures that the migration operator is the adjoint of the
forward modeling counterpart.
Yunsong Huang
2013-09-22
![\includegraphics[width=3.35in]{fig/phaseShiftFlowchart}](img499.png)
![]() per layer can be decomposed into a succession
of four linear operators
per layer can be decomposed into a succession
of four linear operators
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() . First, the seismic wavefield
. First, the seismic wavefield
![]() at
at ![]() is
transformed to the wavenumber
is
transformed to the wavenumber ![]() domain by the Fourier operator
domain by the Fourier operator
![]() .
Second, the phase-shift operator
.
Second, the phase-shift operator
![]() is applied to the wavefield in the
is applied to the wavefield in the
![]() domain:
domain:
![]() applies to the case of `backward propagation', or downward
continuation of the data, as illustrated in Figure B.1(c).
This ensures that the migration operator is the adjoint of the
forward modeling counterpart.
applies to the case of `backward propagation', or downward
continuation of the data, as illustrated in Figure B.1(c).
This ensures that the migration operator is the adjoint of the
forward modeling counterpart.