


Next: Numerical Results
Up: Filtering the GDM Kernel
Previous: Horizontal Reflector Model
Contents
If the reflector is vertically oriented and
the source and receiver are
to the right of the reflector,
then a dip filter can be used
to separate leftgoing and rightgoing terms.
Migrating a single trace associated with the
vertical reflector model in Figure ![[*]](crossref.png) c gives the migration image in
Figure
c gives the migration image in
Figure ![[*]](crossref.png) d. Only the ellipse-like feature is
desired, which can be isolated by
replacing the
upgoing reflection Green's
function
d. Only the ellipse-like feature is
desired, which can be isolated by
replacing the
upgoing reflection Green's
function
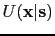 by the rightgoing one
by the rightgoing one
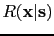 in equation
in equation ![[*]](crossref.png) to give
to give
Dip filtering can be used
to separate the leftgoing and rightgoing waves
in the migration kernel, and
the image of the desired Kirchhoff kernel is shown in
Figure ![[*]](crossref.png) a. The dot-product of this kernel
with the data can be used to get the desirable
image of the vertical reflector.
Figures
a. The dot-product of this kernel
with the data can be used to get the desirable
image of the vertical reflector.
Figures ![[*]](crossref.png) b-d respectively correspond to the 1st, 3rd, and 4th terms in equation
b-d respectively correspond to the 1st, 3rd, and 4th terms in equation ![[*]](crossref.png) ,
which are the undesirable parts for migration.
,
which are the undesirable parts for migration.
Figure:
Wavepaths in Figure ![[*]](crossref.png) d separated by dip filtering the migration
kernel
d separated by dip filtering the migration
kernel
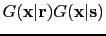 associated
with the vertical reflector model in Figure
associated
with the vertical reflector model in Figure ![[*]](crossref.png) c.
c.
|
|



Next: Numerical Results
Up: Filtering the GDM Kernel
Previous: Horizontal Reflector Model
Contents
Ge Zhan
2013-07-08
![$\displaystyle \int \int_{B} d \omega dx_r~\omega^2~[\tilde d^{t}({\bf {r}}\vert...
...bf {r}})]^*~[D^{t}({\bf {x}}\vert{\bf {s}})+R^{r}({\bf {x}}\vert{\bf {s}})]^* ,$](img81.png)
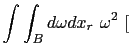
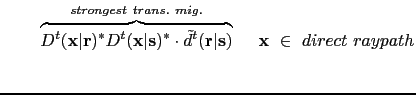
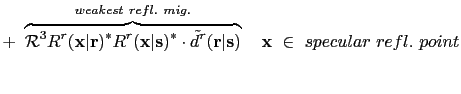
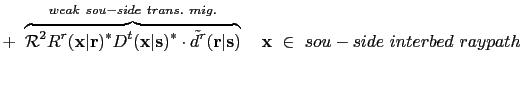
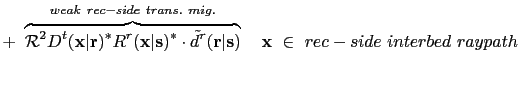
![$\displaystyle +~ \overbrace{\mathcal RD^{t}({\bf {x}}\vert{\bf {r}})^* D^{t}({\...
...\bf {s}})}^{strong~refl.~mig.}~]
~~~{\bf {x}}~\in~ specular~refl.~pt.+ellipse.$](img85.png)
![[*]](crossref.png) c gives the migration image in
Figure
c gives the migration image in
Figure ![[*]](crossref.png) d. Only the ellipse-like feature is
desired, which can be isolated by
replacing the
upgoing reflection Green's
function
d. Only the ellipse-like feature is
desired, which can be isolated by
replacing the
upgoing reflection Green's
function
![[*]](crossref.png) to give
to give
![[*]](crossref.png) a. The dot-product of this kernel
with the data can be used to get the desirable
image of the vertical reflector.
Figures
a. The dot-product of this kernel
with the data can be used to get the desirable
image of the vertical reflector.
Figures ![[*]](crossref.png) b-d respectively correspond to the 1st, 3rd, and 4th terms in equation
b-d respectively correspond to the 1st, 3rd, and 4th terms in equation ![[*]](crossref.png) ,
which are the undesirable parts for migration.
,
which are the undesirable parts for migration.