



Next: Antialiasing Filter for Kirchhoff
Up: Introduction and Method
Previous: Introduction and Method
Contents
This migration operation can also be interpreted as
a dot-product
of the kernel fingerprint
 with the CSG fingerprint
with the CSG fingerprint
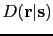 (Schuster, 2002),
and the result is
(Schuster, 2002),
and the result is
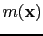 .
If the trial image point is at an actual scatterer,
then the fingerprints of the CSG and migration kernel
will be a good match and the dot-product will return a large value.
If the trial image point is far from any reflector, then the CSG and kernel fingerprints
will be mismatched and the dot-product will yield a low magnitude.
This description defines the dot-product interpretation
of migration, and I will now refer to
.
If the trial image point is at an actual scatterer,
then the fingerprints of the CSG and migration kernel
will be a good match and the dot-product will return a large value.
If the trial image point is far from any reflector, then the CSG and kernel fingerprints
will be mismatched and the dot-product will yield a low magnitude.
This description defines the dot-product interpretation
of migration, and I will now refer to
 and
and
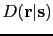 as kernel and data fingerprints, respectively.
as kernel and data fingerprints, respectively.
Ge Zhan
2013-07-08