Next: Antialiasing Filter for Reverse-time
Up: Introduction and Method
Previous: Migration as Fingerprint Matching
Contents
The antialiasing condition for the KM operator
(Gray, 1992; Lumley et al., 1994; Abma et al., 1999; Biondi, 2001;
Zhang et al., 2003)
says that the local slope 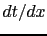 (e.g., computed from the traveltime table)
of the associated hyperbola diffraction curve in
(e.g., computed from the traveltime table)
of the associated hyperbola diffraction curve in 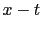 space should
satisfy the Nyquist sampling criterion:
space should
satisfy the Nyquist sampling criterion:
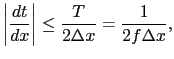 |
|
|
(10) |
where 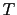 is the minimum period in the data at frequency
is the minimum period in the data at frequency 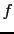 ,
and
,
and 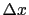 is the input trace spacing.
If this condition is not satisfied for any
is the input trace spacing.
If this condition is not satisfied for any 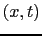 sample in the CSG,
the local portion of this trace at time
sample in the CSG,
the local portion of this trace at time  is high-cut filtered to
is high-cut filtered to
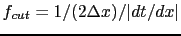 to eliminate the offending high-frequency components.
to eliminate the offending high-frequency components.
Figure:
Migration kernels plotted in data space as colored hyperbolas for
a) primary and b) primary+multiple events
associated with shallow (green) and deep (pink) trial image points.
The best match between the data (black hyperbolas)
and migration curves (pink and green) is when the trial image point
is near the actual scatterer's position; the
dot-product between the migration kernel and data
fingerprints will give the greatest value when the trial image point is at the actual scatterer's location.
|
|




Next: Antialiasing Filter for Reverse-time
Up: Introduction and Method
Previous: Migration as Fingerprint Matching
Contents
Ge Zhan
2013-07-08