



Next: Numerical Results
Up: Introduction and Method
Previous: Antialiasing Filter for Kirchhoff
Contents
If
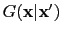 is computed by
a finite-difference solution to the wave equation, then
equation
is computed by
a finite-difference solution to the wave equation, then
equation ![[*]](crossref.png) defines the RTM formula.
Its traditional implementation (Stolt and Benson, 1986) is to backpropagate the data and
take the zero-lag correlation of it with the forward propagated field
to get
defines the RTM formula.
Its traditional implementation (Stolt and Benson, 1986) is to backpropagate the data and
take the zero-lag correlation of it with the forward propagated field
to get
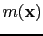 .
An alternative implementation+interpretation of RTM
is provided by generalized diffraction-stack migration (GDM).
Schuster (2002) showed that the RTM image at
.
An alternative implementation+interpretation of RTM
is provided by generalized diffraction-stack migration (GDM).
Schuster (2002) showed that the RTM image at 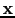 can be implemented as a dot-product
of the kernel
fingerprint
can be implemented as a dot-product
of the kernel
fingerprint
![$ {\mathcal F}^{-1}[G({\bf {r}}\vert{\bf {x}})G({\bf {x}}\vert{\bf {s}})]$](img110.png) with that of the CSG fingerprint
with that of the CSG fingerprint
![$ {\mathcal F}^{-1}[D({\bf {r}}\vert{\bf {s}})]$](img111.png) , where
, where
![$ {\mathcal F}^{-1}[~]$](img112.png) represents the inverse Fourier transform.
In either the RTM or GDM implementations, the resulting migration images are identical.
represents the inverse Fourier transform.
In either the RTM or GDM implementations, the resulting migration images are identical.
As an example, Figure ![[*]](crossref.png) b shows that the kernel fingerprint consists
of several hyperbolas for a specified image point
b shows that the kernel fingerprint consists
of several hyperbolas for a specified image point 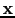 .
The early arriving hyperbola is for the primary scattering and the later one
is associated with a multiple.
Therefore, the antialiasing strategy for RTM consists of the following:
.
The early arriving hyperbola is for the primary scattering and the later one
is associated with a multiple.
Therefore, the antialiasing strategy for RTM consists of the following:
- Define
![$ g({\bf {r}},t\vert{\bf {x}},0)={\mathcal F}^{-1} [G({\bf {r}}\vert{\bf {x}})]$](img113.png) .
Use a finite-difference solution to the space-time wave equation
to compute
.
Use a finite-difference solution to the space-time wave equation
to compute
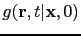 for a source at
for a source at 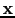 and receiver at
and receiver at 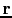 . Here
. Here 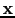 is in the model space.
is in the model space.
- Convolve
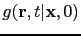 with
with
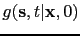 to get the kernel fingerprint (RTM migration kernel)
to get the kernel fingerprint (RTM migration kernel)
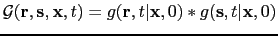 , where
, where 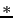 denotes temporal convolution.
The convolution results are the colored-line hyperbolas shown in Figure
denotes temporal convolution.
The convolution results are the colored-line hyperbolas shown in Figure ![[*]](crossref.png) b.
b.
- Apply local low-pass filters to every time sample of
this kernel so that the antialiasing condition
![[*]](crossref.png) is satisfied.
Denote this
filtered kernel fingerprint as
is satisfied.
Denote this
filtered kernel fingerprint as
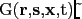 .
.
- Take dot-products of the migration kernel
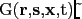 with the CSG in the time domain
with the CSG in the time domain
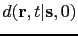 to get the
prestack migration image
to get the
prestack migration image
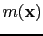 for a single shot at
for a single shot at  .
The resulting image will be free of aliasing artifacts.
.
The resulting image will be free of aliasing artifacts.




Next: Numerical Results
Up: Introduction and Method
Previous: Antialiasing Filter for Kirchhoff
Contents
Ge Zhan
2013-07-08
![[*]](crossref.png) b shows that the kernel fingerprint consists
of several hyperbolas for a specified image point
b shows that the kernel fingerprint consists
of several hyperbolas for a specified image point ![[*]](crossref.png) defines the RTM formula.
Its traditional implementation (Stolt and Benson, 1986) is to backpropagate the data and
take the zero-lag correlation of it with the forward propagated field
to get
defines the RTM formula.
Its traditional implementation (Stolt and Benson, 1986) is to backpropagate the data and
take the zero-lag correlation of it with the forward propagated field
to get
![[*]](crossref.png) b shows that the kernel fingerprint consists
of several hyperbolas for a specified image point
b shows that the kernel fingerprint consists
of several hyperbolas for a specified image point ![]() .
The early arriving hyperbola is for the primary scattering and the later one
is associated with a multiple.
Therefore, the antialiasing strategy for RTM consists of the following:
.
The early arriving hyperbola is for the primary scattering and the later one
is associated with a multiple.
Therefore, the antialiasing strategy for RTM consists of the following:
![[*]](crossref.png) b.
b.
![[*]](crossref.png) is satisfied.
Denote this
filtered kernel fingerprint as
is satisfied.
Denote this
filtered kernel fingerprint as