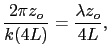Introduction

The classical limit of spatial resolution in 2D seismic imaging is governed by the range of scattering wavenumber vectors $\boldsymbol{k} = (k_x,k_z)$ in the recorded primary reflection energy. This means that higher frequencies and larger values of $k_x$ lead to better lateral resolution of a point scatterer in a migration image. Equivalently, wider reflection angles and wider source-receiver apertures will lead to better lateral resolution. This idea is quantified by the poststack Rayleigh resolution formula (Elmore and Heald, 1969):

$$\Delta x =2x= \frac{2\pi z_o}{k (4L)} = \frac{\lambda z_o}{4L},$$ (11)

where $z_0$ is the depth of the point scatterer, $L$ is the aperture width of the poststack traces, $k$ is the wavenumber magnitude, and $\Delta x$ is the minimum lateral distance between adjacent point scatterers that can just be resolved in a poststack migration image.

To achieve a better horizontal resolution for a fixed aperture width, multiple scattering events should be used. For a complex medium, the multiple scattered energy arrives from a wider range of incidence angles than primaries, and so can yield a much wider range of $\boldsymbol{k}$ values. This enhanced resolution from multiple scattering is now known as superresolution (Blomgren et al., 2002; Lerosey et al., 2007 and many others). Recent studies at the wavelength scale of seismic exploration show that noticeably higher lateral resolution can be achieved with certain types of field data (Hanafy et al., 2009). For the Hanafy et al. (2009) tests, the field data consist of traces excited by deeply buried seismic sources which is far from the practice of seismic exploration where the sources are near the free surface. The question remains: can superresolution be achieved by migrating seismic data recorded by current technology?

To partly answer this question, I develop a modified form of reverse-time migration (RTM) (Schuster, 2002) and show with synthetic data that it can yield superresolution images if the velocity model is known with high accuracy. However, a drawback is the introduction of noise into the image.

This chapter is divided into three parts: method, examples, and conclusions. I briefly introduce the method first, then I demonstrate synthetic examples on the 2D SEG/EAGE salt model to show the feasibility of superresolution with seismic data. At the end, I draw some conclusions.