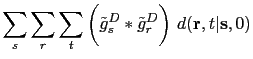Next: Summary
Up: Migration of Multiple Scattered
Previous: Method
Contents
I tested the GDM method on the 2D SEG/EAGE salt model (see Figure ![[*]](crossref.png) a)
and associated synthetic data computed by FD solutions to the 2D acoustic wave equation.
The data include shot gathers generated by 323 shots with a peak-frequency of 13 Hz. There are 176
receivers in each shot gather, and shot and receiver intervals are 48.8 m and 24.4 m, respectively. There are
1001 time samples with a time interval of 0.008 s in each trace. To reduce
the computation time, I only focus on the small region
below the salt shown in Figure
a)
and associated synthetic data computed by FD solutions to the 2D acoustic wave equation.
The data include shot gathers generated by 323 shots with a peak-frequency of 13 Hz. There are 176
receivers in each shot gather, and shot and receiver intervals are 48.8 m and 24.4 m, respectively. There are
1001 time samples with a time interval of 0.008 s in each trace. To reduce
the computation time, I only focus on the small region
below the salt shown in Figure ![[*]](crossref.png) b.
b.
Figure ![[*]](crossref.png) a shows a typical Green's function generated by the wave equation
solver.
I first mute everything but the early-arrivals of the Green's function
(Zhou and Schuster, 2002),
and the migration kernel is calculated by convolving only the traces with the early-arrivals (Figure
a shows a typical Green's function generated by the wave equation
solver.
I first mute everything but the early-arrivals of the Green's function
(Zhou and Schuster, 2002),
and the migration kernel is calculated by convolving only the traces with the early-arrivals (Figure ![[*]](crossref.png) b),
which only employs a few periods of the wavefront.
The GDM image of the early-arrivals is shown in Figure
b),
which only employs a few periods of the wavefront.
The GDM image of the early-arrivals is shown in Figure ![[*]](crossref.png) a.
For comparison, I also implement the
GDM using the entire wavefield (Figure
a.
For comparison, I also implement the
GDM using the entire wavefield (Figure ![[*]](crossref.png) a) instead of just using the early-arrivals.
The migration result is shown in Figure
a) instead of just using the early-arrivals.
The migration result is shown in Figure ![[*]](crossref.png) b.
The wavefront image (Figure
b.
The wavefront image (Figure ![[*]](crossref.png) a) and the entire waveform image (Figure
a) and the entire waveform image (Figure ![[*]](crossref.png) b) are almost identical.
The reason is that the direct waves, or the early-arrivals in the Green's function are the
strongest events, the amplitude of which is about two orders-of-magnitude larger than that of the multiples.
Therefore, after the dot-product and stacking processes, the contributions of the weak-amplitudes (i.e., later arrivals) of the multiples
in the migration
image are concealed by the relatively strong-amplitudes of the direct waves and primaries.
This can be mathematically demonstrated in the following way.
b) are almost identical.
The reason is that the direct waves, or the early-arrivals in the Green's function are the
strongest events, the amplitude of which is about two orders-of-magnitude larger than that of the multiples.
Therefore, after the dot-product and stacking processes, the contributions of the weak-amplitudes (i.e., later arrivals) of the multiples
in the migration
image are concealed by the relatively strong-amplitudes of the direct waves and primaries.
This can be mathematically demonstrated in the following way.
Figure:
Velocity model used in the synthetic tests.
|
|
Figure:
Synthetic Green's function and its separation in time.
a) A typical bandlimited Green's function generated from the 2D SEG/EAGE salt model.
The dashed box shows b) the early-arrivals.
c) The Green's function only containing multiples.
|
|
Figure:
Migration results using the GDM method.
a) Migration image constructed from migration kernel formed by convolving the early-arrivals.
b) Migration image using all of the arrivals to form a migration kernel.
c) Migration image using only multiples in the migration kernel.
d) The optimal stack of a) and c).
|
|
The Green's function shown in Figure ![[*]](crossref.png) a can be divided into two parts, direct waves (Figure
a can be divided into two parts, direct waves (Figure ![[*]](crossref.png) b) and multiples (Figure
b) and multiples (Figure ![[*]](crossref.png) c):
c):
where the superscripts 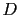 and
and 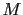 stand for direct waves and multiples.
And the subscripts
stand for direct waves and multiples.
And the subscripts  and
and 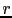 denote
the source-side and receiver-side Green's function, respectively.
Plugging equation
denote
the source-side and receiver-side Green's function, respectively.
Plugging equation ![[*]](crossref.png) into
into ![[*]](crossref.png) , I get
, I get
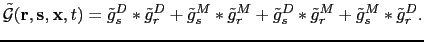 |
|
|
(15) |
It is clear that the generalized diffraction-stack migration using the early-arrivals of the Green's function is nothing but
the dot-product of the recorded shot gathers with the first term of the migration kernel
in equation ![[*]](crossref.png) .
The direct waves are strong
compared to multiples, so the other three terms in equation
.
The direct waves are strong
compared to multiples, so the other three terms in equation ![[*]](crossref.png) ,
especially the second term, is very small compared to the first term. Therefore, when I apply the GDM using the
entire wavefield of the Green's function, I get nearly the same result as applying the GDM using early-arrivals only.
,
especially the second term, is very small compared to the first term. Therefore, when I apply the GDM using the
entire wavefield of the Green's function, I get nearly the same result as applying the GDM using early-arrivals only.
Inspired by the above analysis, I calculate the GDM images separately, one
using the direct-wave migration kernel and the other using the multiple migration kernel; and then
compute the
optimal weighting factor before stacking the two images together.
Here I only consider the first two parts of equation ![[*]](crossref.png) and neglect the last two terms. This is illustrated by
rewriting equation
and neglect the last two terms. This is illustrated by
rewriting equation ![[*]](crossref.png) as
as
where 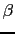 is the optimal weighting factor for stacking migration images
in a small window. Hence, the contribution from
both the direct waves and multiples are equalized which in theory should result in a more detailed migration image.
is the optimal weighting factor for stacking migration images
in a small window. Hence, the contribution from
both the direct waves and multiples are equalized which in theory should result in a more detailed migration image.
Figure ![[*]](crossref.png) c shows the GDM result using the Green's function only containing multiples
(Figure
c shows the GDM result using the Green's function only containing multiples
(Figure ![[*]](crossref.png) c); this migration kernel is
generated by muting the early-arrivals in the dashed box shown in Figure
c); this migration kernel is
generated by muting the early-arrivals in the dashed box shown in Figure ![[*]](crossref.png) a and keeping all multiple arrivals. This
indeed represents the second term in equation
a and keeping all multiple arrivals. This
indeed represents the second term in equation ![[*]](crossref.png) . Comparing with Figures
. Comparing with Figures ![[*]](crossref.png) a and
a and ![[*]](crossref.png) b, I get a migration image with better
illumination of the subsalt structure and inevitably more noise as well.
After estimating the optimal factor
b, I get a migration image with better
illumination of the subsalt structure and inevitably more noise as well.
After estimating the optimal factor 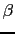 , I stack the two images from the
primary reflection migration (Figure
, I stack the two images from the
primary reflection migration (Figure ![[*]](crossref.png) a)
and the migration of multiples (Figure
a)
and the migration of multiples (Figure ![[*]](crossref.png) c) following equation
c) following equation ![[*]](crossref.png) ; and I finally get the optimal
stacked image shown in Figure
; and I finally get the optimal
stacked image shown in Figure ![[*]](crossref.png) d.
Note that more noise is introduced in Figure
d.
Note that more noise is introduced in Figure ![[*]](crossref.png) d
using this method, but such artifacts can be attenuated with a least-squares migration algorithm.
d
using this method, but such artifacts can be attenuated with a least-squares migration algorithm.




Next: Summary
Up: Migration of Multiple Scattered
Previous: Method
Contents
Ge Zhan
2013-07-08
![[*]](crossref.png) a shows a typical Green's function generated by the wave equation
solver.
I first mute everything but the early-arrivals of the Green's function
(Zhou and Schuster, 2002),
and the migration kernel is calculated by convolving only the traces with the early-arrivals (Figure
a shows a typical Green's function generated by the wave equation
solver.
I first mute everything but the early-arrivals of the Green's function
(Zhou and Schuster, 2002),
and the migration kernel is calculated by convolving only the traces with the early-arrivals (Figure ![[*]](crossref.png) b),
which only employs a few periods of the wavefront.
The GDM image of the early-arrivals is shown in Figure
b),
which only employs a few periods of the wavefront.
The GDM image of the early-arrivals is shown in Figure ![[*]](crossref.png) a.
For comparison, I also implement the
GDM using the entire wavefield (Figure
a.
For comparison, I also implement the
GDM using the entire wavefield (Figure ![[*]](crossref.png) a) instead of just using the early-arrivals.
The migration result is shown in Figure
a) instead of just using the early-arrivals.
The migration result is shown in Figure ![[*]](crossref.png) b.
The wavefront image (Figure
b.
The wavefront image (Figure ![[*]](crossref.png) a) and the entire waveform image (Figure
a) and the entire waveform image (Figure ![[*]](crossref.png) b) are almost identical.
The reason is that the direct waves, or the early-arrivals in the Green's function are the
strongest events, the amplitude of which is about two orders-of-magnitude larger than that of the multiples.
Therefore, after the dot-product and stacking processes, the contributions of the weak-amplitudes (i.e., later arrivals) of the multiples
in the migration
image are concealed by the relatively strong-amplitudes of the direct waves and primaries.
This can be mathematically demonstrated in the following way.
b) are almost identical.
The reason is that the direct waves, or the early-arrivals in the Green's function are the
strongest events, the amplitude of which is about two orders-of-magnitude larger than that of the multiples.
Therefore, after the dot-product and stacking processes, the contributions of the weak-amplitudes (i.e., later arrivals) of the multiples
in the migration
image are concealed by the relatively strong-amplitudes of the direct waves and primaries.
This can be mathematically demonstrated in the following way.
![$\displaystyle \sum_{s}\sum_{r}\sum_{t}\bigg[\tilde{g}_s^D \ast \tilde{g}_r^D + ...
...igg(\tilde{g}_s^M \ast \tilde{g}_r^M\bigg)\bigg]~d({\bf {r}},t\vert{\bf {s}},0)$](img164.png)