



Next: Phase-encoded Generalized Diffraction-stack Migration
Up: Theory
Previous: Theory
Contents
The phase-encoded multisource traces are first formed by summing the encoded traces
from all mono-frequency shot gathers.
Here I assume a fixed spread geometry.
Then the phase-encoded RTM method back-projects every multisource trace
and migrating with the following formula
where
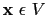 ,
,
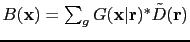 is the back-projected reflection wavefield and
is the back-projected reflection wavefield and
 is the forward-modeled multisource wavefield at the trial
image point
is the forward-modeled multisource wavefield at the trial
image point 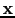 . Also,
the
. Also,
the 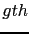 component of the encoded multisource data
component of the encoded multisource data 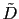 is denoted by
is denoted by
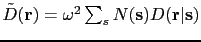 , where
, where
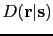 represents the recorded single-source
shot gather, and
represents the recorded single-source
shot gather, and 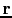 indicates the receiver position on the surface.
The data and migration operators are in the frequency domain at angular
frequency
indicates the receiver position on the surface.
The data and migration operators are in the frequency domain at angular
frequency 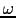 , and
, and 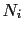 is mapped to the function
is mapped to the function
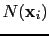 .
.




Next: Phase-encoded Generalized Diffraction-stack Migration
Up: Theory
Previous: Theory
Contents
Ge Zhan
2013-07-08
![$\displaystyle \sum_r \sum_s
G({\bf {x}}\vert{\bf {r}})^* \tilde{D}({\bf {r}})
[N({\bf {s}})G({\bf {x}}\vert{\bf {s}})]^* ,$](img190.png)
![$\displaystyle \sum_r \overbrace{G({\bf {x}}\vert{\bf {r}})^*\tilde{D}({\bf {r}}...
...{s} \overbrace{[N({\bf {s}})G({\bf {x}}\vert{\bf {s}})]^*}^{forward~propagate},$](img191.png)