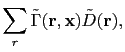Phase-encoded Generalized Diffraction-stack Migration

Phase-encoded GDM is equivalent to the phase-encoded RTM but is implemented in a different order; i.e.,

$$m({\bf {x}}) = \sum_r \sum_s G({\bf {x}}\vert{\bf {r}})^* \tilde{D}({\bf {r}}) [N({\bf {s}})G({\bf {x}}\vert{\bf {s}})]^* ,$$

$$= \sum_r \bigg[ \sum_s \overbrace{ N({\bf {s}})G({\bf {x}}\vert{\bf... ...^*G({\bf {x}}\vert{\bf {s}})^*}^{migration~kernel} \bigg] \tilde{D}({\bf {r}}),$$

$$= \sum_r \tilde{\Gamma}({\bf {r}},{\bf {x}}) \tilde{D}({\bf {r}}),$$ (22)

where

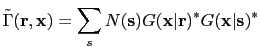$$\tilde{\Gamma}({\bf {r}},{\bf {x}}) = \sum_s N({\bf {s}})G({\bf {x}}\vert{\bf {r}})^*G({\bf {x}}\vert{\bf {s}})^*$$ (23)

is the convolution of the receiver-side Green's function and the source-side Green's function followed by phase-encoding. It is also known as the multisource migration operator or multisource focusing kernel (Schuster, 2002).