



Next: Theory of Generalized Diffraction-stack
Up: Generalized Diffraction-stack Migration: A
Previous: Theory of Diffraction-stack Migration
Contents
If
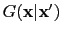 is computed by a finite-difference solution to the wave equation in the frequency domain,
then the equation of prestack reverse-time migration (RTM) can be obtained by right shifting the
square brackets
in equation
is computed by a finite-difference solution to the wave equation in the frequency domain,
then the equation of prestack reverse-time migration (RTM) can be obtained by right shifting the
square brackets
in equation ![[*]](crossref.png)
The traditional implementation of prestack RTM (Stolt and Benson, 1986) is to backpropagate the data and
take the zero-lag correlation of it with the forward propagated source wavefield
to get
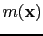 . This is illustrated in Figure
. This is illustrated in Figure ![[*]](crossref.png) .
.
Figure:
The standard reverse-time migration (RTM) image is obtained by computing the
zero-lag correlation of the forward-propagated source wavefield a) with the back-projected data b). The scattering point at 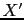 shows up in c) after
applying the imaging condition.
shows up in c) after
applying the imaging condition.
|
|
Ge Zhan
2013-07-08
![$\displaystyle \sum_{\omega} \sum_r \alpha(\omega,{\bf {x}},{\bf {r}},{\bf {s}})...
...ace{[G({\bf {r}}\vert{\bf {x}})^*D({\bf {r}}\vert{\bf {s}})]}^{back~propagate}.$](img17.png)
![[*]](crossref.png)
![]() . This is illustrated in Figure
. This is illustrated in Figure ![[*]](crossref.png) .
.