Hess Salt Model

I first test the TTI RTM code on the synthetic data generated with the Hess salt model. This model consists of a VTI velocity stratification where the P-wave velocity, epsilon, and delta distributions are shown in Figure 2.1. By simply setting the tilt angle to be 30 degrees instead of zero, the synthetic TTI dataset is produced using equation 2.1. To avoid shear wave artifacts, a small smoothly tapered circular region with 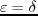$\varepsilon = \delta$ is set around the source (Duveneck et al., 2008).

Figure 2.1: Hess salt models used in the TTI RTM test: distributions for the P-wave velocity (top), epsilon (middle) and delta (bottom). Dip angle theta is constant and equals 30 degrees.

The TTI RTM code is then tested on the Hess synthetic data. Both isotropic ( 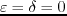$\varepsilon=\delta=0$ ) RTM and TTI RTM are implemented. Since the tilt angle is constant, this test is free of instability problems. Figure 2.2 shows the RTM results, where the migration images are plotted with the background velocity model to check the RTM accuracy. The image from the isotropic migration suffers from a horizontally spatial shift, and is poorly focused. The migration artifacts and imaging errors are caused by ignoring the anisotropy effects. But the TTI RTM provides a more accurate migration image consistent with the velocity model.

Figure 2.2: TTI RTM images plotted with the background P-wave velocity model. On the bottom is the TTI RTM image of the synthetic data generated with a 30 degrees tilt angle. For comparison, the same data is migrated by conventional isotropic RTM and the result is shown on the top. The TTI RTM image matches the structure quite well, but on the isotropic one, image blurring and mispositioning is present.