To validate the proposed TTI decoupled equations, several synthetic modeling and RTM examples are demonstrated. For comparison, results from the TTI coupled equations (equation 2 in Fletcher et al. (2009)) are also presented.
First, I demonstrate the proposed algorithm using an impulse response.
Figure 3.2 shows time snapshots of wave
propagation at time ![]() in a 2D homogeneous TTI medium with
in a 2D homogeneous TTI medium with
![]() ,
,
![]() ,
,
![]() and
and
![]() .
By solving the TTI coupled equations with
.
By solving the TTI coupled equations with ![]() set to zero, Figure 3.2a
is obtained where we can clearly see an elliptical P wavefront as well as a diamond-shape SV wavefront.
Figure 3.2b shows a same time snapshot
as that in Figure 3.2a, but with a nonzero SV wave velocity (
set to zero, Figure 3.2a
is obtained where we can clearly see an elliptical P wavefront as well as a diamond-shape SV wavefront.
Figure 3.2b shows a same time snapshot
as that in Figure 3.2a, but with a nonzero SV wave velocity (
![]() ).
By adding a finite SV wave velocity,
SV wave triplications are successfully removed
but the shear wave, which is considered as an artifact in P wave modeling and migration,
is still present in Figure 3.2b.
Figure 3.2c and 3.2d demonstrate the separated
P wave and SV wave snapshots from the TTI decoupled equations.
Compared to Figure 3.2b, it is obvious that
Figure 3.2c only has the P wave component
and Figure 3.2d only contains the SV wave component.
Therefore, the proposed TTI decoupled equations offer a better modeling and
migration alternative since the P wave and SV wave modes are separated.
Since the SV wave is usually considered as an artifact in conventional P wave modeling and migration,
I only focus on the TTI decoupled P wave equation in the following discussion.
).
By adding a finite SV wave velocity,
SV wave triplications are successfully removed
but the shear wave, which is considered as an artifact in P wave modeling and migration,
is still present in Figure 3.2b.
Figure 3.2c and 3.2d demonstrate the separated
P wave and SV wave snapshots from the TTI decoupled equations.
Compared to Figure 3.2b, it is obvious that
Figure 3.2c only has the P wave component
and Figure 3.2d only contains the SV wave component.
Therefore, the proposed TTI decoupled equations offer a better modeling and
migration alternative since the P wave and SV wave modes are separated.
Since the SV wave is usually considered as an artifact in conventional P wave modeling and migration,
I only focus on the TTI decoupled P wave equation in the following discussion.
|
|
Second, I show some modeling examples using a 2D inhomogeneous wedge model
where sharp contrasts exist in all parameter models (Figure 3.3).
The model shown here is the same as the one used by Duveneck and Bakker (2011),
which is originally designed to compare abilities of different approaches
that deal with the instability problem in TTI media.
To avoid SV waves generated from the source,
they placed an isotropic layer on the top. I did so as to compare, but it is not necessary for my algorithm.
Figure 3.4a shows the interface in sharp contrast of this anisotropic model.
Figure 3.4b and Figure 3.4c are snapshots at
time ![]() computed
using the TTI coupled equations with
computed
using the TTI coupled equations with ![]() and
and
![]() , respectively.
SV wavefront appears to come out from the top interface of the wedge. Using the decoupled P wave equation, I get a clean wavefield snapshot without any
shear wave contamination (Figure 3.4d).
Figure 3.5 compares the same snapshots at time
, respectively.
SV wavefront appears to come out from the top interface of the wedge. Using the decoupled P wave equation, I get a clean wavefield snapshot without any
shear wave contamination (Figure 3.4d).
Figure 3.5 compares the same snapshots at time ![]() .
Notice that the instabilities start to appear in Figure 3.5b for
the
.
Notice that the instabilities start to appear in Figure 3.5b for
the ![]() case. Adding a nonzero shear wave velocity can mitigate the instability problem
and thus stabilize the wave propagation (Figure 3.5c), but SV wavefronts are clearly
present.
Figure 3.5d from the TTI decoupled P wave equation solution is not only stable but also
much cleaner than Figure 3.5c since the equation does not contain any shear wave components.
Figure 3.6 displays wavefield snapshots at a later time (
case. Adding a nonzero shear wave velocity can mitigate the instability problem
and thus stabilize the wave propagation (Figure 3.5c), but SV wavefronts are clearly
present.
Figure 3.5d from the TTI decoupled P wave equation solution is not only stable but also
much cleaner than Figure 3.5c since the equation does not contain any shear wave components.
Figure 3.6 displays wavefield snapshots at a later time (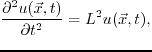 ).
Even with a nonzero shear wave velocity, the wave propagation
becomes
unstable for long propagation times (Figure 3.6c).
However, the decoupled P
wave equation proceeds with a stable response and the wavefield exits the computation grid without
ever becoming unstable (Figure 3.6d).
).
Even with a nonzero shear wave velocity, the wave propagation
becomes
unstable for long propagation times (Figure 3.6c).
However, the decoupled P
wave equation proceeds with a stable response and the wavefield exits the computation grid without
ever becoming unstable (Figure 3.6d).
|
|
|
|
|
|
|
|
To further verify the proposed algorithm,
I implement an anisotropic RTM using the TTI decoupled P wave equation.
The BP 2007 TTI dataset is used in my RTM test.
Figure 3.7 shows the parameter values for
![]() ,
, ![]() ,
, ![]() and
and ![]() of a small region of the 2D BP TTI model.
Rapid variation of the tilt angle shown here presents challenges to TTI RTM.
Before doing migration, a modeling test showing the instability problem is demonstrated.
Figure 3.8 displays forward modeling snapshots at time
of a small region of the 2D BP TTI model.
Rapid variation of the tilt angle shown here presents challenges to TTI RTM.
Before doing migration, a modeling test showing the instability problem is demonstrated.
Figure 3.8 displays forward modeling snapshots at time 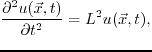 .
Notice that numerical instabilities arise in Figure 3.8b from the
place where rapid dip variations exist (see Figure 3.8a).
Using a finite shear wave velocity
(
.
Notice that numerical instabilities arise in Figure 3.8b from the
place where rapid dip variations exist (see Figure 3.8a).
Using a finite shear wave velocity
(
![]() ) can
stabilize wave propagation and the resulting snapshot is displayed
in Figure 3.8c.
Notice that there are some visible SV wave artifacts present in Figure 3.8c.
Instead of using the TTI coupled equation with a nonzero shear wave velocity,
I use the TTI decoupled P wave equation given by equation 3.11 to propagate the wavefield
and the result is shown in Figure 3.8d.
The wavefield is as stable as Figure 3.8c but is clean due to the complete isolation of the SV wave component in the P wave equation.
The TTI decoupled P wave equation provides a stable result
and is completely independent of variations in the anisotropic parameter models.
In addition, it is absolutely free of any SV wave components.
) can
stabilize wave propagation and the resulting snapshot is displayed
in Figure 3.8c.
Notice that there are some visible SV wave artifacts present in Figure 3.8c.
Instead of using the TTI coupled equation with a nonzero shear wave velocity,
I use the TTI decoupled P wave equation given by equation 3.11 to propagate the wavefield
and the result is shown in Figure 3.8d.
The wavefield is as stable as Figure 3.8c but is clean due to the complete isolation of the SV wave component in the P wave equation.
The TTI decoupled P wave equation provides a stable result
and is completely independent of variations in the anisotropic parameter models.
In addition, it is absolutely free of any SV wave components.
|
|
Finally, RTM results of the corresponding region are presented. Figure 3.9 compares VTI and TTI reverse time migration. Figure 3.9a is obtained using the VTI decoupled P wave equation described in equations 3.4. Due to ignoring the tilt angle, imaging of dipping events is severely affected and they seem to be mispositioned and defocused in the VTI RTM image. Using the TTI decoupled P wave equation given by equations 3.11, a TTI RTM image is achieved and the resulting image is shown in Figure 3.9b. It is clear that events are well positioned and focused at interface boundaries in the TTI RTM image using the TTI decoupled P wave equation. This is further demonstrated in Figure 3.10 which shows zoom views of Figure 3.9a and 3.9b.