


Next: VTI pure P-wave equation
Up: Equations
Previous: Equations
Contents
The constant-density acoustic wave equation in isotropic media is
 |
(41) |
where
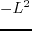 is the pressure wavefield at spatial location
is the pressure wavefield at spatial location
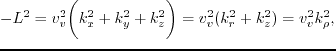 and time
and time 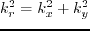 ;
;
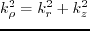 ,
,
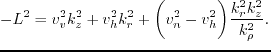 is the P-wave velocity in the medium,
and
is the P-wave velocity in the medium,
and 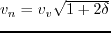 is the Laplacian defined as
is the Laplacian defined as
 .
Efficient numerical solutions of the wave equation on a discrete grid is my main interest.
To solve the discretized version of equation 4.1, I approximate the temporal
(left) and spatial (right) derivatives in the equation,
where the time derivative can be approximated by
a second-order finite-difference approximation
.
Efficient numerical solutions of the wave equation on a discrete grid is my main interest.
To solve the discretized version of equation 4.1, I approximate the temporal
(left) and spatial (right) derivatives in the equation,
where the time derivative can be approximated by
a second-order finite-difference approximation
![$\displaystyle u(\vecx ,t+\dt ) = 2u(\vecx ,t) - u(\vecx ,t-\dt ) - \dt ^2 \bigg[ -L^2 u(\vecx ,t) \bigg],$](img97.png) |
(42) |
where 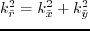 denotes the length of a discrete time step.
denotes the length of a discrete time step.
The pseudospectral method is known as a highly accurate scheme
for approximating the Laplacian operator.
In doing so, the numerical errors in the solution of the wave equation
are only dominated by the temporal discretization.
For the isotropic case, the 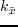 operator in equation 4.2 can be expressed
in the wavenumber domain
operator in equation 4.2 can be expressed
in the wavenumber domain
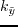 |
(43) |
where 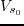 is the velocity of a wave traveling vertically along the axis of symmetry;
is the velocity of a wave traveling vertically along the axis of symmetry;
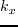 ,
, 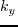 and
and 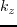 are spatial wavenumbers,
are spatial wavenumbers,
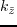 , and
, and
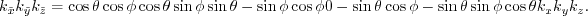 .
.



Next: VTI pure P-wave equation
Up: Equations
Previous: Equations
Contents
Ge Zhan
2013-07-09
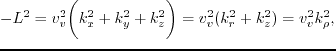 and time
and time 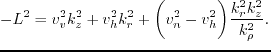 is the P-wave velocity in the medium,
and
is the P-wave velocity in the medium,
and ![]() operator in equation 4.2 can be expressed
in the wavenumber domain
operator in equation 4.2 can be expressed
in the wavenumber domain