VTI pure P-wave equation

In the case of VTI, based on Harlan (1995) and later rediscovered by Etgen and Brandsberg-Dahl (2009), Crawley et al. (2010), Pestana et al. (2012) and Zhan et al. (2012) where they started from the exact phase velocity expression for VTI media, equation 4.3 becomes

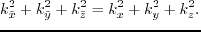$$-L^2 = v_v^2 k_z^2 + v_h^2 k_r^2 + \bigg( v_n^2 - v_h^2 \bigg) \frac{k_r^2k_z^2}{k_{\rho}^2}.$$ (44)

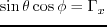Here, $v_n=v_v\sqrt{1+2\delta}$ and $v_h=v_v\sqrt{1+2\varepsilon}$ represent the normal moveout (NMO) velocity and the P-wave velocity in the horizontal direction, respectively; 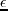$\delta$ and $\varepsilon$ are Thomsen's (1986) parameters.

The resulting anisotropic wave equation derived in this way is known as the decoupled or pure P-wave equation, where the P-wave and shear-wave are separated and there is no spurious shear-wave artifacts in the P-wave simulation.