


Next: 1 Rapid Expansion Method
Up: Thesis
Previous: Bibliography
Contents
0 3D TTI Decoupled Equations
Rewriting equations 3.6 using the relation
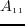 yields
yields
![$\displaystyle \left\{ \begin{array}{ll} \omega^2=V^2_{p_0} \bigg[ (k^2_r + k^2_...
...at{k}^4_z}{k^2_r+k^2_z} \bigg] \;\;\;\;\;\mbox{(SV wave)} \end{array} \right. .$](img169.png) |
(01) |
Plugging equations 3.8 into equations A.1,
we get the approximated P wave and SV wave dispersion relations for TTI media in 3D case
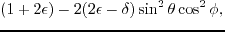 |
|
|
(02) |
where the differential operator 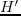 is defined as
is defined as
Here 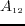 and
and 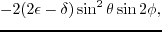 are coefficients related to Thomsen's anisotropy parameters (
are coefficients related to Thomsen's anisotropy parameters (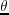 and
and 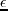 ),
dip and azimuth (
),
dip and azimuth (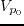 and
and 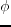 ), and the ratio of SV wave and P wave velocities (
), and the ratio of SV wave and P wave velocities (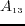 /
/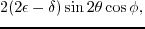 )
)
The corresponding decoupled P wave and SV wave equations in the time-wavenumber domain for 3D TTI media are
Figure A.1 shows a snapshot of an impulse response
at time 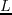 in a 3D homogeneous TTI medium with
in a 3D homogeneous TTI medium with
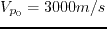 ,
,
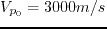 ,
,
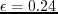 ,
,
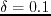 and
and
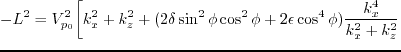 using the above TTI decoupled P wave equation.
using the above TTI decoupled P wave equation.
For the case of HTI, 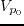 is 90 degrees and
is 90 degrees and
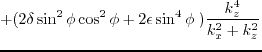 becomes zero. In this case, equation A.3 is simplified with coefficients
becomes zero. In this case, equation A.3 is simplified with coefficients
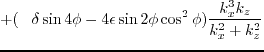 and
and
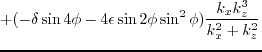 all becoming zero.
all becoming zero.
For the case of tilted elliptical isotropy,
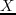 and many coefficients in equations
A.2 and A.3 go to zero, for examples, all
and many coefficients in equations
A.2 and A.3 go to zero, for examples, all
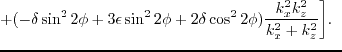 and
and
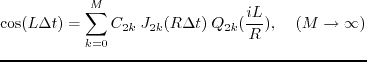 and
and
 .
.
Figure:
Wavefield snapshots at time 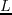 in a 3D homogeneous TTI medium
with
in a 3D homogeneous TTI medium
with
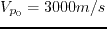 ,
,
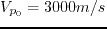 ,
,
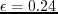 ,
,
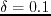 and
and
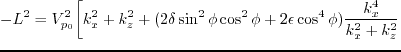 .
A point source is located in the center at
.
A point source is located in the center at
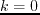 .
(a), (b) and (c) are 2D
.
(a), (b) and (c) are 2D 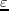 -
-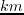 ,
, 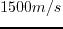 -
-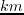 and
and 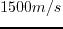 -
- slices across the source location, respectively.
slices across the source location, respectively.
|
|



Next: 1 Rapid Expansion Method
Up: Thesis
Previous: Bibliography
Contents
Ge Zhan
2013-07-09
![]() yields
yields
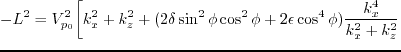 using the above TTI decoupled P wave equation.
using the above TTI decoupled P wave equation.
![]() is 90 degrees and
is 90 degrees and
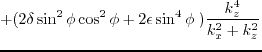 becomes zero. In this case, equation A.3 is simplified with coefficients
becomes zero. In this case, equation A.3 is simplified with coefficients
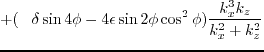 and
and
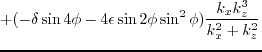 all becoming zero.
all becoming zero.
![]() and many coefficients in equations
A.2 and A.3 go to zero, for examples, all
and many coefficients in equations
A.2 and A.3 go to zero, for examples, all
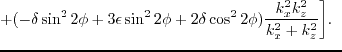 and
and
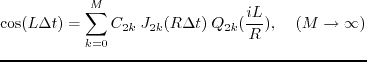 and
and
![]() .
.