1    Rapid Expansion Method

The solution of equation 3.11 is given by

$$p(t+\Delta t)=-p(t-\Delta t)+2\cos(L \Delta t)p(t),$$ (11)

where pseudo-differential operator $L$ is defined as

$$-L^2=V^2_{p_0}\bigg[ k^2_x+k^2_z + ( 2\delta\sin^2\phi\cos^2\phi + 2\epsilon\cos^4\phi )\frac{k^4_x}{k^2_x+k^2_z}$$

$$+ ( 2\delta\sin^2\phi\cos^2\phi + 2\epsilon\sin^4\phi \;)\frac{k^4_z}{k^2_x+k^2_z}$$

$$+ (\;\;\; \delta\sin4\phi - 4\epsilon\sin2\phi\cos^2\phi )\frac{k^3_xk_z}{k^2_x+k^2_z}$$

$$+ ( -\delta\sin4\phi - 4\epsilon\sin2\phi\sin^2\phi )\frac{k_xk^3_z}{k^2_x+k^2_z}$$

$$+ ( -\delta\sin^22\phi + 3\epsilon\sin^22\phi + 2\delta\cos^22\phi )\frac{k^2_xk^2_z}{k^2_x+k^2_z}\bigg].\;\;$$ (12)

An efficient orthogonal polynomial series expansion for the cosine function in equation B.1 was presented by Tal-Ezer et al. (1987)

$$\cos(L\Delta t)=\sum_{k=0}^M{C_{2k}\;J_{2k}(R\Delta t)\;Q_{2k}(\frac{iL}{R})}, \;\;\;\;(M\rightarrow\infty)$$ (13)

where $C_{2k}=1$ for $k=0$ and $C_{2k}=2$ for $k>0$ . $R$ is chosen as the largest eigenvalue of $L^2$ . $J_{2k}$ is the Bessel function of the first kind order and $Q_{2k}$ are the modified Chebyshev polynomials that satisfy the following recurrence relations

$$Q_0(\frac{iL}{R}) = I,$$

$$Q_2(\frac{iL}{R}) = I-\frac{2L^2}{R^2},$$

$$Q_{2k+2}(\frac{iL}{R}) = 2(I-\frac{2L^2}{R^2})Q_{2k}-Q_{2k-2}.$$

Here, is the identity matrix.

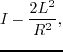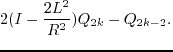For 2D isotropic wave propagation, the value of $R$ is given by

where is the highest P wave velocity in the grid. For anisotropic case, should be replaced by and is the maximum absolute value from the $\epsilon$ model.

The summation in equation B.3 is known to converge exponentially for , therefore the summation can be safely truncated using a value of slightly greater than . Pestana and Stoffa (2010) have demonstrated that when , which means only two terms are kept in the summation, this approximation of the cosine function using the Chebyshev polynomials results in the 2nd-order in time finite-difference scheme. When , the operator term is included, this approximation is equivalent to the 4th-order finite-different scheme proposed by Dablain (1986) and Etgen (1986).