



Next: Phase encoding
Up: Theory
Previous: Numerical Scheme: Linear Inversion
Contents
Two types of preconditioners are used to regularize the iterative solution represented by equation (2.12). The first one is a high-pass filter in the space domain. It is constructed according to scale-space theory (Lindeberg, 1994), where the basic idea is to obtain a low-wavenumber component of the image (gradient) by convolving it with a 2D/3D Gaussian function. The Gaussian function is parameterized by a scalar 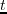 , which controls the smoothness of the image after convolution. The implementation of high pass filtering requires the low-wavenumber component to be subtracted from the original image.
For numerical implementation, the pyramid approximation (Burt and Adelson, 1983) is used for the filter. A small [0.25 0.5 0.25] filter is recursively applied along the
, which controls the smoothness of the image after convolution. The implementation of high pass filtering requires the low-wavenumber component to be subtracted from the original image.
For numerical implementation, the pyramid approximation (Burt and Adelson, 1983) is used for the filter. A small [0.25 0.5 0.25] filter is recursively applied along the 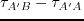 and
and 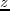 directions to approximate the Gaussian function. The number of iterations in applying this small filter controls the smoothness of the image after convolution. Then, the filtered image is subtracted from the original to get the high-wavenumber component of the original image.
During the LSM iterations, a proper passband should be defined in the wavenumber domain that separates the artifacts and the model update. Then a high-pass filter should be applied at the early iterations to remove the low-wavenumber back-scattering artifacts.
Note a preconditioner should be symmetric positive definite (SPD) for an iterative conjugate gradient algorithm. However, ensuring this high-pass filter is SPD is not automatic so this preconditioner is not used after about 5 iterations.
directions to approximate the Gaussian function. The number of iterations in applying this small filter controls the smoothness of the image after convolution. Then, the filtered image is subtracted from the original to get the high-wavenumber component of the original image.
During the LSM iterations, a proper passband should be defined in the wavenumber domain that separates the artifacts and the model update. Then a high-pass filter should be applied at the early iterations to remove the low-wavenumber back-scattering artifacts.
Note a preconditioner should be symmetric positive definite (SPD) for an iterative conjugate gradient algorithm. However, ensuring this high-pass filter is SPD is not automatic so this preconditioner is not used after about 5 iterations.
The second preconditioner is the illumination compensation, which is an approximation to the inverse of the diagonal Hessian. This preconditioner enjoyed early use by Beydoun and Mendes (1989) and Luo and Schuster (1991). Plessix and Mulder (2004) provide a thorough review of its performance and properties. The illumination compensation is a diagonal matrix with positive elements, so it is always SPD and is safe to use for every iteration in LSM.




Next: Phase encoding
Up: Theory
Previous: Numerical Scheme: Linear Inversion
Contents
Wei Dai
2013-07-10