Estimate of Computational Cost

For a fixed-spread acquisition survey with 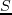$S$ shots in total, the computational cost of conventional RTM is approximately 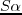$S\alpha$ , where 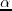$\alpha$ is the cost of one migration operation. On the other hand, for multisource LSRTM with 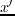$N$ sub-supergathers and 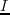$I$ iterations, the computational cost is about 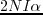$2NI\alpha$ , assuming that each iteration of LSRTM takes twice the computation cost of one RTM operation. The speedup of phase encoding LSRTM relative to conventional RTM can be estimated as

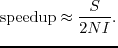$$\textrm{speedup} \approx \frac{S}{2NI}.$$ (215)

Therefore, Figures 2.4(b), (c), and (d) show a speedup of 30, 7.5, and 3.75, respectively.

The above estimation is done with the assumption that for LSRTM the computational cost of each iteration is twice that for conventional RTM. so the speedup is the optimal result which maybe difficult to achieve for practical applications. There are two reasons: (1) complicated line search methods can be used with more computation to enhance the robustness of LSRTM; (2) in real applications, some optimization techniques, that can be applied to conventional sources RTM, may not be available for multisource data.