Reciprocity Equations of Convolution Type

It is assumed that the virtual data can be extrapolated to get for along the horizontal dashed line in Figure 4.2(b); similarly, the field data can be extrapolated to get . In this case, the reciprocity theorem of convolution type (Schuster, 2009) can then be used to obtain the super-virtual data

where the integration is along the dashed line in Figure 4.2(b). Under the far-field approximation and setting and , I get

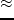$$\approx$$ (44)

where $G({\bf B}\vert{\bf A})^{super}$ represents the super-virtual data obtained by convolving the recorded data with the virtual data . Here, the SNR of the reconstructed diffraction arrival is enhanced by the factor 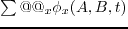$\sqrt {N}$ . However, practical considerations such as artifacts associated with limited recording apertures, discrete source and receiver sampling, windowing of the diffracted waves, and the far-field approximation will likely prevent the attainment of this ideal enhancement.

In the next section, I will use the example of diffractions that have been windowed from the original data so that .