Multisource Migration

From equation , the supergather migration operator is defined as the adjoint of the supergather modeling operator,

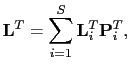$$\textbf{L}^{T}=\sum_{i=1}^{S}\textbf{L}_{i}^{T}\textbf{P}_{i}^{T},$$ (5)

so that the supergather migration image is

$$\textbf{m}_{mig} = \textbf{L}^{T}\textbf{d}=\textbf{L}^{T}\sum_{i=1}^{S}\textbf{P}_{i}\textbf{L}_{i}\textbf{m}$$

$$= \sum_{j=1}^{S}\textbf{L}_{j}^{T}\textbf{P}_{j}^{T}\sum_{i=1}^{S}\textbf{P}_{i}\textbf{L}_{i}\textbf{m}$$

$$= \sum_{i=1}^{S}\sum_{j=1}^{S}\textbf{L}_{j}^{T}\textbf{P}_{j}^{T}\textbf{P}_{i}\textbf{L}_{i}\textbf{m}$$

$$= \overbrace{\sum_{i=1}^{S}\textbf{L}_{i}^{T}\textbf{L}_{i}\textbf{... ...}_{j}^{T}\textbf{P}_{j}^{T}\textbf{P}_{i}\textbf{L}_{i}\textbf{m}}^{crosstalk},$$ (6)

consisting of two terms: the first term is the standard migration image and the second term is the crosstalk noise introduced by multisource blending of shot gathers. The magnitude of the crosstalk term for a variety of different phase encoding functions is derived in Schuster et al. (2011).