



Next: Numerical Implementation
Up: Theory
Previous: Multisource Migration
Contents
In order to suppress crosstalk noise to an acceptable level when the number of multiple sources 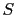 is large, I solve equation
is large, I solve equation ![[*]](file:~/utilities/latex2html/icons/crossref.png) in the least-squares sense (Dai and Schuster, 2009; Dai et al., 2009). That is, define the objective function as
in the least-squares sense (Dai and Schuster, 2009; Dai et al., 2009). That is, define the objective function as
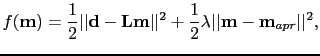 |
(7) |
so that, an optimal
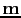 is sought to minimize the objective function in equation
is sought to minimize the objective function in equation ![[*]](file:~/utilities/latex2html/icons/crossref.png) .
In equation
.
In equation ![[*]](file:~/utilities/latex2html/icons/crossref.png) , Tikhonov regularization (Tikhonov and Arsenin, 1977) is used and
, Tikhonov regularization (Tikhonov and Arsenin, 1977) is used and  is the regularization parameter, determined by a trial and error method. Smoothness constraints in the form of second-order derivatives of the model function can expedite convergence (Kühl and Sacchi, 2003) and partly overcome the problems associated with errors in the velocity model.
is the regularization parameter, determined by a trial and error method. Smoothness constraints in the form of second-order derivatives of the model function can expedite convergence (Kühl and Sacchi, 2003) and partly overcome the problems associated with errors in the velocity model.
With the assumption that nothing is known about
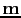 ,
,
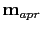 is set to be equal to zero. The model
is set to be equal to zero. The model
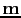 that minimizes equation
that minimizes equation ![[*]](file:~/utilities/latex2html/icons/crossref.png) can be found by a gradient type optimization method
can be found by a gradient type optimization method
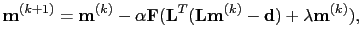 |
(8) |
where
 is the gradient,
is the gradient,
 is a preconditioning matrix and
is a preconditioning matrix and 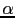 is the step length. As both the forward modeling and migration operators are linear and adjoint to each other, the analytical step length formula can be used. Alternatively, in order to improve the robustness of the MLSM algorithm, a quadratic line search method is carried out with the current model and two trial models. In this study, I use the conjugate gradient (CG) method, which generally converges faster than the steepest decent method. Moreover, static encoding is used where the encoding functions are the same for every iteration to reduce the I/O cost. Boonyasiriwat and Schuster (2010) show that dynamic encoding (encoding functions are changed at every iteration) is more effective in 3D multisource full waveform inversion and so dynamic encoding results are presented as well. To ensure the convergence of MLSM, the migration velocity should be close to the true velocity model.
is the step length. As both the forward modeling and migration operators are linear and adjoint to each other, the analytical step length formula can be used. Alternatively, in order to improve the robustness of the MLSM algorithm, a quadratic line search method is carried out with the current model and two trial models. In this study, I use the conjugate gradient (CG) method, which generally converges faster than the steepest decent method. Moreover, static encoding is used where the encoding functions are the same for every iteration to reduce the I/O cost. Boonyasiriwat and Schuster (2010) show that dynamic encoding (encoding functions are changed at every iteration) is more effective in 3D multisource full waveform inversion and so dynamic encoding results are presented as well. To ensure the convergence of MLSM, the migration velocity should be close to the true velocity model.




Next: Numerical Implementation
Up: Theory
Previous: Multisource Migration
Contents
Wei Dai
2013-07-10
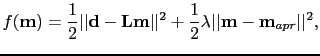
![]() ,
,
![]() is set to be equal to zero. The model
is set to be equal to zero. The model
![]() that minimizes equation
that minimizes equation ![]() can be found by a gradient type optimization method
can be found by a gradient type optimization method