Numerical Results

The multisource least-squares migration algorithm wth Kirchhoff modeling and adjoint operators is tested on synthetic data generated by a Born modeling method for the 2D SEG/EAGE salt model. Figure  shows the reflectivity model calculated from the velocity model using vertical rays and constant density assumptions; the true velocity model is used for migration. The ocean bottom reflector is muted in order to better illustrate the deep structure, and 320 sources and 320 receivers are deployed on the surface with the same sampling interval of 18.3 m. The modeling parameters are listed in Table 1 (see Appendix A for the meaning of deblurring filter parameters), where the deblurring filter is only applied at the first two iterations to provide a good initial model for the inversion. The regularization parameter is chosen based on a trial and error method and is reduced by half after each iteration. Regularization is important for attenuating crosstalk noise and high-frequency noise associated with the deblurring filter.

Table 2.1: Modeling parameters for conventional sources simulation.

Model size	645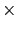$\times$ 150	Src Wavelet	Ricker
Grid interval	9.14 m	Peak freq.	50 Hz
Src number	320	Src interval	18.3 m
Rec. number	320	Rec. interval	18.3 m
Trace length	4 sec	Regularization	1.0e-7
Subsec. size	5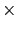$\times$ 5 pts	Filter size	3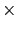$\times$ 3 pts

Figure 2.2: 2D SEG/EAGE salt model (reflectivity).