To simulate multisource data, conventional sources data are encoded and blended together to form a small number of supergathers. The 320 shot gathers are separated into different clusters of supergathers, where each supergather in a cluster is formed by stacking a unique set of shot gathers together to form the following data sets: thirty-two 10-shot supergathers, sixteen 20-shot supergathers, eight 40-shot supergathers, four 80-shot supergathers, two 160-shot supergathers and one 320-shot supergather. Each shot gather has a random time shift applied to it with a standard deviation equal to about seven times the dominant period of the source wavelet. All the random time shifts are generated by a random number generator that honors a uniform probability distribution. Figure ![]() shows the Kirchhoff migration images from all the experiments. Consistent with equation
shows the Kirchhoff migration images from all the experiments. Consistent with equation ![]() , these results show that decreasing the number of supergather leads to increasing levels of crosstalk.
, these results show that decreasing the number of supergather leads to increasing levels of crosstalk.
![\includegraphics[width=6.0in]{./chap2.lsm.img/Figure5.eps}](img52.png)
|
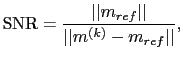 |
(12) |
![\includegraphics[width=4.0in]{./chap2.lsm.img/Figure6.eps}](img62.png)
|
![\includegraphics[width=6.0in]{./chap2.lsm.img/Figure7.eps}](img63.png)
|
For the case where ![]() is much greater than 1, Figure
is much greater than 1, Figure ![]() presents the migration images where the input data consist of only one supergather (
presents the migration images where the input data consist of only one supergather (![]() , in equation
, in equation ![]() ) but there are different numbers of shot gathers in the supergather: (a)
) but there are different numbers of shot gathers in the supergather: (a) ![]() =40, (b)
=40, (b) ![]() =80 and (c)
=80 and (c) ![]() =160. These results along with Figure
=160. These results along with Figure ![]() f demonstrate that the SNRs of these migration images are mostly independent of the number of shot gathers in the supergather. At first glance, this result appears contradictory to intuition because the migration of a 160-shot supergather might be expected to yield a less noisy image than a 80-shot supergather. However, the 160-shot supergather has a higher crosstalk noise level (by a factor of
f demonstrate that the SNRs of these migration images are mostly independent of the number of shot gathers in the supergather. At first glance, this result appears contradictory to intuition because the migration of a 160-shot supergather might be expected to yield a less noisy image than a 80-shot supergather. However, the 160-shot supergather has a higher crosstalk noise level (by a factor of ![]() ) than the 80-shot supergather, which cancels the
) than the 80-shot supergather, which cancels the ![]() SNR enhancement in migrating a 160-shot supergather. The key point here is that increasing the number of unique supergathers is more effective at SNR enhancement than increasing the number of unique shot gathers per supergather.
SNR enhancement in migrating a 160-shot supergather. The key point here is that increasing the number of unique supergathers is more effective at SNR enhancement than increasing the number of unique shot gathers per supergather.
According to equation ![]() , even a single 320-shot supergather can be used to get an accurate image if the number of iterations is large enough. To verify this prediction, Figure
, even a single 320-shot supergather can be used to get an accurate image if the number of iterations is large enough. To verify this prediction, Figure ![]() a-c shows the MLSM images after iteratively migrating a 320-shot supergather; here, the deblurring filter is applied to stabilize and speed up the convergence. It is clear that the image quality increases with the number of iterations. After 60 iterations, the MLSM image is of high quality and mostly free of migration artifacts and crosstalk. It indicates that MLSM can accurately estimate the model even when hundreds of shots are blended together in the processing step, and it does not require too many iterations. Moreover, since the SNR is proportional to
a-c shows the MLSM images after iteratively migrating a 320-shot supergather; here, the deblurring filter is applied to stabilize and speed up the convergence. It is clear that the image quality increases with the number of iterations. After 60 iterations, the MLSM image is of high quality and mostly free of migration artifacts and crosstalk. It indicates that MLSM can accurately estimate the model even when hundreds of shots are blended together in the processing step, and it does not require too many iterations. Moreover, since the SNR is proportional to ![]() ,
, ![]() being the number of supergathers, the crosstalk noise will be more effectively suppressed when there is more than one supergather.
being the number of supergathers, the crosstalk noise will be more effectively suppressed when there is more than one supergather.
![\includegraphics[width=3.0in]{./chap2.lsm.img/Figure8.eps}](img67.png)
|
![\includegraphics[width=6.0in]{./chap2.lsm.img/Figure9.eps}](img68.png)
|