



Next: Least-squares Migration with Prestack
Up: Multisource Least-squares Migration and
Previous: Deblurring filter
Contents
Signal-to-noise Ratio
Consider an observed trace 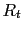 , consisting of a signal trace
, consisting of a signal trace 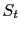 and zero-mean independent and identically-distributed
and zero-mean independent and identically-distributed![[*]](file:~/utilities/latex2html/icons/footnote.png) noise
noise 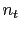 of variance
of variance  , as in
, as in
When 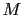 such observed traces are drawn and stacked, I get
such observed traces are drawn and stacked, I get
where 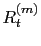 denotes the
denotes the  th random realization of the signal trace
th random realization of the signal trace 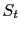 . (
. ( 's are still i.i.d.) The signal and the noise part of the stacked trace
's are still i.i.d.) The signal and the noise part of the stacked trace
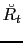 are denoted by
are denoted by
respectively. Note that the root mean squared (rms) amplitude of the stacked signal
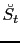 is
is
where
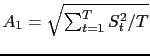 is the rms amplitude of the signal trace
is the rms amplitude of the signal trace 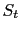 and the second equality follows from equation B.2; and
and the second equality follows from equation B.2; and 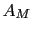 is defined as the rms amplitude of the
is defined as the rms amplitude of the 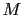 -fold stacked signal
-fold stacked signal
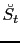 , growing in proportion to
, growing in proportion to 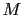 , according to equation B.4. The rms amplitude of the stacked noise
, according to equation B.4. The rms amplitude of the stacked noise
 ,
,  , is defined as
, is defined as
where  denotes expectation, the second equality follows because
denotes expectation, the second equality follows because 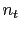 's are identically-distributed, the third equality follows from equation B.3, the fourth
equality follows because
's are identically-distributed, the third equality follows from equation B.3, the fourth
equality follows because  's are zero-mean and independent, and the last equality follows because
's are zero-mean and independent, and the last equality follows because  's are identically-distributed with variance
's are identically-distributed with variance  . Equation B.5 shows that
. Equation B.5 shows that  grows in proportion to
grows in proportion to  .
.
Finally, The SNR of
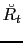 is defined as the ratio of rms amplitude of signal over that of noise (Papoulis, 1991),
is defined as the ratio of rms amplitude of signal over that of noise (Papoulis, 1991),
which exhibits a  enhancement.
enhancement.




Next: Least-squares Migration with Prestack
Up: Multisource Least-squares Migration and
Previous: Deblurring filter
Contents
Wei Dai
2013-07-10
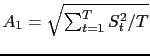 is the rms amplitude of the signal trace
is the rms amplitude of the signal trace ![]() is defined as the ratio of rms amplitude of signal over that of noise (Papoulis, 1991),
is defined as the ratio of rms amplitude of signal over that of noise (Papoulis, 1991),