



Next: Mathematical Derivation with Adjoint
Up: Multisource Least-squares Migration and
Previous: Signal-to-noise Ratio
Contents
Least-squares Migration with Prestack Image
In least-squares migration, the goal is to solve the over-determined system of equations
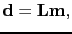 |
(77) |
where
 is the data vector,
is the data vector,
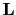 matrix represents the forward modeling operator, and
matrix represents the forward modeling operator, and
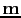 is the model vector,
and the corresponding normal equation is
is the model vector,
and the corresponding normal equation is
 |
(78) |
The direct least-squares solution is
![$\displaystyle \textbf{m}=[\textbf{L}^T\textbf{L}]^{-1}\textbf{L}^T\textbf{d}.$](img339.png) |
(79) |
Assuming a dataset with three shots, each of dimension
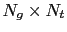 , the total length of the data vector is
, the total length of the data vector is
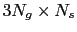 . If the model vector is of the size
. If the model vector is of the size
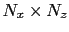 , the dimension of equation C.1 will be
, the dimension of equation C.1 will be
![$\displaystyle \left [ \textbf{d} \right ]^{3N_{g}N_{s}}=\left [ \textbf{L}\right ]^{3N_{g}N_{s} \times N_{x}N_{z}} \left [ \textbf{m} \right ]^{N_{x}N_{z}}.$](img343.png) |
(80) |
For example, if the three shots are
 ,
,
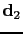 , and
, and
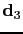 , each with the length of
, each with the length of
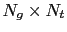 , the above equation can be rewritten as
, the above equation can be rewritten as
![$\displaystyle \begin{bmatrix}
\textbf{d}_1\\
\textbf{d}_2\\
\textbf{d}_3
...
...\\
\textbf{L}_2 \\
\textbf{L}_3
\end{bmatrix}\left [ \textbf{m} \right ],$](img347.png) |
(81) |
where
 ,
,
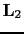 , and
, and
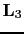 are the forward modeling operator associated with each shot respectively. Here,
are the forward modeling operator associated with each shot respectively. Here,
 denotes the shot gather for the
denotes the shot gather for the  shot.
shot.
When the least-squares migration is performed with a stacked image as shown in equation C.5, the answer
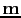 in equation C.3 is the solution to the whole problem. In this dissertation, I propose to introduce an ensemble of prestack images
in equation C.3 is the solution to the whole problem. In this dissertation, I propose to introduce an ensemble of prestack images
 |
(82) |
into the inversion scheme, so that the system of equations becomes
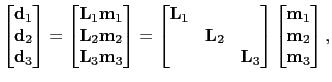 |
(83) |
where
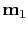 ,
,
 , and
, and
 are the migration image associated for each shot respectively, each with the size of
are the migration image associated for each shot respectively, each with the size of
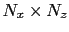 .
The direct solution to the equation C.7 is
.
The direct solution to the equation C.7 is
![$\displaystyle \begin{bmatrix}
\textbf{m}_1\\
\textbf{m}_2\\
\textbf{m}_3
\end...
...\
[\textbf{L}^T_3\textbf{L}_3]^{-1}\textbf{L}^T_{3}\textbf{d}_3
\end{bmatrix}.$](img356.png) |
|
|
(84) |
It is clear that the solution
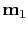 ,
,
 , and
, and
 are independent of each other. By introducing the prestack image into the inversion, I solve three small problems instead of one big problem, thus make it possible to find stable solution when the equations are not consistent with each other in the case of wrong migration velocity.
are independent of each other. By introducing the prestack image into the inversion, I solve three small problems instead of one big problem, thus make it possible to find stable solution when the equations are not consistent with each other in the case of wrong migration velocity.




Next: Mathematical Derivation with Adjoint
Up: Multisource Least-squares Migration and
Previous: Signal-to-noise Ratio
Contents
Wei Dai
2013-07-10
![]() , the total length of the data vector is
, the total length of the data vector is
![]() . If the model vector is of the size
. If the model vector is of the size
![]() , the dimension of equation C.1 will be
, the dimension of equation C.1 will be
![]() in equation C.3 is the solution to the whole problem. In this dissertation, I propose to introduce an ensemble of prestack images
in equation C.3 is the solution to the whole problem. In this dissertation, I propose to introduce an ensemble of prestack images

![$\displaystyle \begin{bmatrix}
\textbf{m}_1\\
\textbf{m}_2\\
\textbf{m}_3
\end...
...\
[\textbf{L}^T_3\textbf{L}_3]^{-1}\textbf{L}^T_{3}\textbf{d}_3
\end{bmatrix}.$](img356.png)