Next: Migration Method Up: Method Previous: Method Contents
Due to frequency division, only a subset of the spectrum will be covered at each source at each iteration,
and so ringy migration artifacts are expected.
An effective method to reduce migration artifacts (Nemeth et al., 1999; Duquet et al., 2000)
is lsm, which
works by iteratively updating a trial model in order to minimize a data
misfit function. A widely adopted misfit function is
the the ![]() norm squared of data error.
In addition, regularization with Cauchy norm (Wang and Sacchi, 2007; Sacchi, 1997; Amundsen, 1991)
is used in this chapter.
In the Bayesian framework (Aster et al., 2005; Debski, 2010), the regularization
corresponds to a negative logarithm of the a priori distribution of the model. The choice of
Cauchy distribution is meant to capture the sparse nature of typical reflectivity models. Following the
Bayesian approach, I write the regularization as
norm squared of data error.
In addition, regularization with Cauchy norm (Wang and Sacchi, 2007; Sacchi, 1997; Amundsen, 1991)
is used in this chapter.
In the Bayesian framework (Aster et al., 2005; Debski, 2010), the regularization
corresponds to a negative logarithm of the a priori distribution of the model. The choice of
Cauchy distribution is meant to capture the sparse nature of typical reflectivity models. Following the
Bayesian approach, I write the regularization as
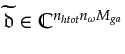 and
and
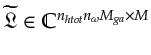 are respectively formed by concatenating
are respectively formed by concatenating
The objective function is then constructed as
As frequency selection encoding could significantly alter the Hessian, the conjugacy condition of cg
cannot be maintained if supergathers are formed with a new frequency selection encoding at each iteration,
a strategy known as `dynamic encoding'.
On one hand, in order to accelerate convergence, and on the other, in order to reduce I/O cost, I adopt a
strategy of a hybrid CG (termed `CG within mimi-batch' in Schraudolph and Graepel, 2002), whereby
supergathers are encoded anew every ![]() iterations.
iterations.
![]() is chosen in this study.
Given fixed supergathers and a fixed
is chosen in this study.
Given fixed supergathers and a fixed ![]() defined in equation 2.38,
defined in equation 2.38, ![]() iterations
are carried out by a CG scheme (outlined in Algorithm 1 in Appendix C).
Then supergathers are randomly encoded again,
iterations
are carried out by a CG scheme (outlined in Algorithm 1 in Appendix C).
Then supergathers are randomly encoded again, ![]() 's are updated, which is
known as the `Iterative Reweighted Least-Squares' method (Scales et al., 1988),
the parameters
's are updated, which is
known as the `Iterative Reweighted Least-Squares' method (Scales et al., 1988),
the parameters ![]() and
and ![]() of the probability distributions are re-estimated through MLE,
and the search direction of CG is reset to negative gradient.
of the probability distributions are re-estimated through MLE,
and the search direction of CG is reset to negative gradient.
Yunsong Huang 2013-09-22