My frequency encoding scheme will now be developed in the same framework of
phase-encoding (Romero et al., 2000), which typically consists of the following
three steps. 1) Different shot gathers are uniquely phase encoded. 2) They are summed together to form
supergathers, which are then 3) migrated all at once.
The first step amounts to multiplying the
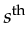 shot gather with a unique
phase encoding function Ns, a step expressed as
shot gather with a unique
phase encoding function Ns, a step expressed as
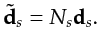 |
(2.5) |
In this dissertation, tilde notes an encoded version of 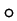 .
Then
.
Then
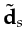 are summed over all sources to give
the encoded supergather
are summed over all sources to give
the encoded supergather
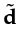 :
:
where the multisource phase-encoded prestack modeling operator is defined as
Finally, the third step involves applying the adjoint
operator
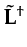 to the encoded supergather
to the encoded supergather
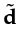 in equation 2.6,
before applying the imaging condition,
to get the migrated image
in equation 2.6,
before applying the imaging condition,
to get the migrated image
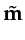 as
as
Here,
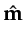 is the sequential shot-gather migration and
is the sequential shot-gather migration and 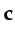 is crosstalk noise.
Equation 2.13 follows assuming the phase encoding function
is crosstalk noise.
Equation 2.13 follows assuming the phase encoding function 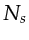 is of pure phase
so that
is of pure phase
so that
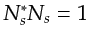 , and equation 2.15 follows from equation 2.4.
, and equation 2.15 follows from equation 2.4.
Note the crosstalk noise, 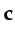 , is the only part of
, is the only part of
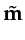 that depends on the random phase
encoding function, over which an ensemble average, denoted by
that depends on the random phase
encoding function, over which an ensemble average, denoted by
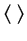 ,
is taken to produce
,
is taken to produce
Yunsong Huang
2013-09-22
![]() to the encoded supergather
to the encoded supergather
![]() in equation 2.6,
before applying the imaging condition,
to get the migrated image
in equation 2.6,
before applying the imaging condition,
to get the migrated image
![]() as
as
![]() , is the only part of
, is the only part of
![]() that depends on the random phase
encoding function, over which an ensemble average, denoted by
that depends on the random phase
encoding function, over which an ensemble average, denoted by
![]() ,
is taken to produce
,
is taken to produce