Theory
The formula for multisource FWI is given
in equation 3.1, where the velocity model is updated at each iteration
and 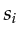 represents the slowness model in each cell.
The frequency selection encoding scheme is described
in Huang and Schuster (2012), and summarized by the following steps.
represents the slowness model in each cell.
The frequency selection encoding scheme is described
in Huang and Schuster (2012), and summarized by the following steps.
- Figure 3.1(a) illustrates the problem, and the first step
is to assign a non-overlapping frequency spectrum to each of the sources.
In Figure 3.1(b), the cyan (red) source is bandlimited around 20 Hz (10 Hz) during the multisource simulation and the supergather is computed.
- In Figure 3.1(c), a bandpass filter is applied to decode the (b) supergather so that the cyan traces
can be separated from the red traces.
In each shot gather, only traces recorded by receivers in a hypothetical marine survey are retained while the others are muted.
- In Figure 3.1(d), the decoded and muted traces are
blended together to give the bandlimited marine supergather. This
procedure is iterated in equation 3.1, except that a unique
non-overlapping frequency is iteratively assigned to each
source. For a sufficient number of iterations,
the full bandwidth of the data is employed at each source.
Figure 3.1:
The solution to the acquisition misfit problem
illustrated in panels (a1) and (a2), is given by
the following steps: (b). the cyan (red) source is bandlimited around 20 Hz (10 Hz) during
the multisource simulation; (c). a bandpass filter is applied to decode these traces so that the cyan traces
can be separated from the red ones. Muting of the specified traces
for a marine geometry is applied. (d). The decoded and muted traces are
blended together to give the bandlimited marine supergather. Now, there is no
aperture mismatch between the simulated and observed supergathers, except that the frequency channels of the
former are a subset of those of the latter.
|
![\includegraphics[width=5.2in]{fwi_fig/illustr}](img289.png) |
To apply the frequency-selection to a fdtd simulation, what are injected at sources (and at receivers when back-propagating the data misfit) are causal sine waves. This causality shows up as transient in received sinusoidal seismograms, causing spectral leakage. To mitigate this problem, assuming the impulse response of the Earth is active only within time 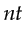 , I run the fdtd simulations over
, I run the fdtd simulations over 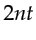 , and keep the responses only within the second
, and keep the responses only within the second 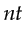 , as illustrated in Figure 3.23.3.
The responses in the second
, as illustrated in Figure 3.23.3.
The responses in the second 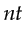 are nearly identical to what is obtained by running the simulation over
are nearly identical to what is obtained by running the simulation over 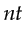 with an input of infinitely long sine waves of period
with an input of infinitely long sine waves of period 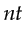 .
Such sine waves are the bases of the dtft of
.
Such sine waves are the bases of the dtft of 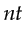 , if performed on the data obtained from the fdtd simulation over
, if performed on the data obtained from the fdtd simulation over 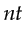 using time-limited source wavelet.
using time-limited source wavelet.
Figure 3.2:
Doubling the simulation
time of fdtd to mitigate the transients when causal sine waves are injected at the inputs, e.g.,
sources or receivers. If a (a) causal sine wave
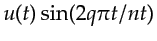 , where
, where 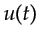 represents a
unit-step function, is convolved with (b) a delayed impulse,
the output is a delayed version of the input signal, plotted in (c), where the black box contains the transient,
while the red box contains the steady-state. If
represents a
unit-step function, is convolved with (b) a delayed impulse,
the output is a delayed version of the input signal, plotted in (c), where the black box contains the transient,
while the red box contains the steady-state. If
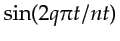 , plotted in (e),
is injected instead, then the output, plotted in (g), would be a scaled and delayed sine wave. Note that
the red box in (g) is identical to that in (c). Due to periodicity in
, plotted in (e),
is injected instead, then the output, plotted in (g), would be a scaled and delayed sine wave. Note that
the red box in (g) is identical to that in (c). Due to periodicity in 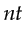 of the input sine wave, in (g)
the black box is identical to the red.
of the input sine wave, in (g)
the black box is identical to the red.
|
![\includegraphics[width=5in]{fwi_fig/2nt_trick}](img296.png) |
This transient-reduction scheme also applies when back-propagating the residual wavefield in forming the gradient of FWI,
as illustrated in Figure 3.3. Note that only the times slices from 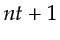 to
to 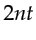 of the
source wavefield need to be reconstructed from the FDTD boundary.
The total number of time steps of FDTD
propagation thus equals
of the
source wavefield need to be reconstructed from the FDTD boundary.
The total number of time steps of FDTD
propagation thus equals
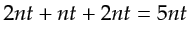 , where the
, where the 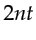 denotes the
total time for the forward-propagation and
back-propagation of the source and residual wavefields, respectively, while the
denotes the
total time for the forward-propagation and
back-propagation of the source and residual wavefields, respectively, while the 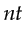 is for reconstruction of the last part of the source wavefield.
This compares to
is for reconstruction of the last part of the source wavefield.
This compares to 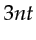 time steps in the standard approach in computing the gradient.
time steps in the standard approach in computing the gradient.
In numerical optimization, after the gradient is computed, Brent's method (Press et al., 2007) is used for the line search.
This takes on average 5 function evaluations, namely, 5 passes of forward-propagation of the source wavefield. Therefore in the standard approach, per iteration of FWI 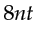 time steps of FDTD propagation are required, whereas in my transient-reduction scheme,
time steps of FDTD propagation are required, whereas in my transient-reduction scheme,
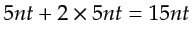 time steps of FDTD propagation are necessary. Roughly, per iteration the latter costs about twice as much as the former does.
time steps of FDTD propagation are necessary. Roughly, per iteration the latter costs about twice as much as the former does.
Yunsong Huang
2013-09-22
![\includegraphics[width=5.2in]{fwi_fig/illustr}](img289.png)
![]() , I run the fdtd simulations over
, I run the fdtd simulations over ![]() , and keep the responses only within the second
, and keep the responses only within the second ![]() , as illustrated in Figure 3.23.3.
The responses in the second
, as illustrated in Figure 3.23.3.
The responses in the second ![]() are nearly identical to what is obtained by running the simulation over
are nearly identical to what is obtained by running the simulation over ![]() with an input of infinitely long sine waves of period
with an input of infinitely long sine waves of period ![]() .
Such sine waves are the bases of the dtft of
.
Such sine waves are the bases of the dtft of ![]() , if performed on the data obtained from the fdtd simulation over
, if performed on the data obtained from the fdtd simulation over ![]() using time-limited source wavelet.
using time-limited source wavelet.
![\includegraphics[width=5in]{fwi_fig/2nt_trick}](img296.png)
![\includegraphics[width=4in]{fwi_fig/2nt_trick_wavefields}](img298.png)
![]() time steps of FDTD propagation are required, whereas in my transient-reduction scheme,
time steps of FDTD propagation are required, whereas in my transient-reduction scheme,
![]() time steps of FDTD propagation are necessary. Roughly, per iteration the latter costs about twice as much as the former does.
time steps of FDTD propagation are necessary. Roughly, per iteration the latter costs about twice as much as the former does.