- ... recording1.1
- This process
of combining several input information signals into one output signal is known
as multiplexing in the communications industry. Recovering
the individual signals from the multiplex signal is known
as demultiplexing.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... operation1.2
- This definition is adjusted
from that in http://en.wikipedia.org/wiki/Decoder.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... outcome2.1
- in MATLAB notation; likewise for the following arrays in this section
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
times2.2
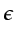 is a small fraction, for instance,
is a small fraction, for instance, 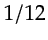 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... size2.3
- measured in the number of complex numbers
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... updates2.4
- Since the Hessian of the objective function is constant given a fixed
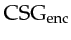 , those
, those 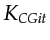 iterations are made using CG.
iterations are made using CG.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... factor2.5
- As
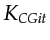 increases,
increases, 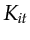 may also have to increase in order to produce acceptable result. Therefore this reduction factor is a bit smaller than
may also have to increase in order to produce acceptable result. Therefore this reduction factor is a bit smaller than 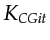 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
size2.6
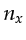 is reduced from the original value of 645 to speed up the FFT.
is reduced from the original value of 645 to speed up the FFT.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... function3.1
- The misfit
function
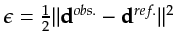 relates to the
relates to the 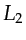 norm of the encoded difference between the
predicted and observed supergathers.
norm of the encoded difference between the
predicted and observed supergathers.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... finite-difference3.2
- A finite-difference simulation of two
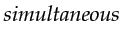 sources (a red source and a dark blue source)
will compute traces everywhere on the surface that are a superposition of the
wavefields from both sources.
sources (a red source and a dark blue source)
will compute traces everywhere on the surface that are a superposition of the
wavefields from both sources.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...fig:2nt3.3
- Only a single
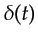 -impulse of the Earth response is shown. Linear superposition generalizes this to an arbitrary impulse response within
-impulse of the Earth response is shown. Linear superposition generalizes this to an arbitrary impulse response within 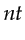 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... smearing4.1
- The seismic amplitude is smeared over the thick ellipse shown in Figure 4.3a,
where the period
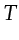 of the trace's source wavelet determines the thickness
of the fat
ellipse in
of the trace's source wavelet determines the thickness
of the fat
ellipse in 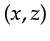 space;
Figure 4.3b illustrates that the minimum
thickness of the fat ellipse as
space;
Figure 4.3b illustrates that the minimum
thickness of the fat ellipse as
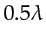 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
residual4.2
- The residual can be either
the traveltime residual or the waveform residual.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
scatterer4.3
- We will assume a 2D model where
the ``point'' source and scatterer are
equivalent to a line source and a line scatterer, with
no field variations along the y-axis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... wavepath4.4
- Dahlen (2004)
refers to the shape of a diving wavepath as a banana.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... wavepaths4.5
- There are two steps for creating an upgoing
reflection wavepath: first, generate the migration image and use the reflectors
as exploding sources that explode at the traveltime from
the source to the reflector. Then, fire off these
exploding reflectors to get the upgoing reflection fields
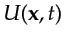 .
The upgoing rabbit ear wavepath is computed by taking the zero-lag correlation between
.
The upgoing rabbit ear wavepath is computed by taking the zero-lag correlation between
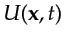 and the backpropagated data
and the backpropagated data
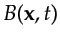 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bed4.6
- The sampling interval between wavenumbers associated with
each order of multiple becomes smaller with thinner beds.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
reflection4.7
- This kernel corresponds to just one of the terms in the
Neummann series expansion of the Lippmann-Schwinger equation (Stolt and Benson, 1986).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... waves11.1
- We exclude the case where the scatterer-diving wave interaction
produces significant diffractions, so that
all source-geophone pairs
see significant diffraction energy, not just changes in the diving-wave
arrival. This would be the case where the scatterer only has a velocity contrast but no impedance contrast.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.