Formulas are derived for the resolution limits of the
migration-data kernels in Figure 4.4,
as well as those for multiple reflections.
They are applicable to
images formed by RTM, LSM, and FWI.
Their salient implications are the following.
- Low- and intermediate-wavenumber information about
the velocity distribution is estimated primarily
by transmission migration of primaries and multiples.
The intermediate wavenumbers can be supplied by
interbed multiples, while the lower wavenumbers are
contained in deep primaries
and free-surface related multiples.
Inverting multiples can be an opportunity for
estimating subsurface velocity information not available in the primary
reflections.
- Inverting diffractions can
provide twice or more the resolution compared to imaging primaries.
Smearing residuals along the transmission wavepath can achieve a
resolution of
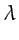 near the diffractor.
This high resolution is observed in MVA tomograms.
On the other hand, diffraction energy
can be more than an order-of-magnitude weaker
than primary energy, so the diffraction data
will be noisier.
near the diffractor.
This high resolution is observed in MVA tomograms.
On the other hand, diffraction energy
can be more than an order-of-magnitude weaker
than primary energy, so the diffraction data
will be noisier.
- Diving waves that bottom out at a certain depth will have a better vertical resolution than horizontal resolution.
Therefore it is important to also invert deep reflections to
increase both the vertical and horizontal resolution. Since
reflections can be an order-of-magnitude weaker
than diving waves, it is recommended that diving waves
be filtered from the data after a sufficient number of
iterations. This might constitute an iterative multi-physics
approach to FWI, where inverting a different type of wavefield
should be emphasized at different depths and iteration
numbers.
- The transmission migration kernels in Figure 4.4a-d are of the same
type as their data kernels. This leads to
velocity updates along the transmission wavepaths. In contrast, the traditional
migration kernel
![$ [G({\bf {g}}\vert{\bf {x}})^{\textrm{dir}}G({\bf {x}}\vert{\bf {s}})^{\textrm{dir}}]^*$](img430.png) in Figure 4.4e is a product
of two Green's functions for direct waves, while
the data kernel is a product of a reflection and a direct-wave Green's function. This mismatch in the type
of kernel does not lead to the traditional wavepath
where seismic energy propagates, but gives
the untraditional wavepath of a fat ellipse. This is the zone
where reflection energy could have originated, i.e., the interface.
in Figure 4.4e is a product
of two Green's functions for direct waves, while
the data kernel is a product of a reflection and a direct-wave Green's function. This mismatch in the type
of kernel does not lead to the traditional wavepath
where seismic energy propagates, but gives
the untraditional wavepath of a fat ellipse. This is the zone
where reflection energy could have originated, i.e., the interface.
The limitation of this study is that it does not take into account
the non-linear effects of evanescent energy (Fleming, 2008)
in determining resolution. Utilizing evanescent energy
with FWI could provide, in theory, resolution much better than 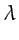 .
It is expected that multiple scattering arrivals
between neighboring subwavelength scatterers might provide the extra resolution needed, but not accounted for
in this current study.
Yunsong Huang
2013-09-22
.
It is expected that multiple scattering arrivals
between neighboring subwavelength scatterers might provide the extra resolution needed, but not accounted for
in this current study.
Yunsong Huang
2013-09-22