Resolution Limits for Reflection Imaging

A seismic migration image is formed by taking the reflection energy arriving at time $\tau_{sx}+\tau_{xg}$ and smearing (Claerbout, 1992) it along the appropriate ellipse in the model-space coordinates ${\bf {x}}$ (see Figure 4.3a). For several traces, the migration image in Figure 4.3b is formed by smearing^4.1 and summing the reflection energy along the appropriate ellipses in the model space.

Figure 4.3: Migration is the smearing and summation of trace amplitudes along the appropriate fat ellipses in $(x,z)$ for each source-receiver pair ${\bf{s}}-{\bf{g}}$ (Claerbout, 1992). Migration of two traces in b) has better spatial resolution than migrating just one trace in a), and the minimum thickness of each fat ellipse is $0.5 \lambda$ , where $T$ is the dominant period of the source wavelet.

It is obvious that the narrowest horizontal slice of the fat ellipse is for a trial image point at the far-left and far-right of the ellipse to give the best horizontal resolution in the reflection migration image. We also see that the narrowest vertical slice is directly beneath the midpoint of the source-receiver pair to give the best vertical resolution. For poststack data, these resolution limits are given on the rightside of Figure 4.4e, which say that the far-offset (near-offset) trace from a trial image point gives the best horizontal (vertical) resolution.

Figure 4.4: Migration-data kernels, associated wavepaths, and approximate resolution limits along the middle of the wavepaths for a-d. Here, the dashed and solid lines in cyan represent the raypaths associated with the conjugated kernels and the data kernels, respectively; the trial image points ${\bf {x}}$ and ${\bf{y}}$ are represented by $\bullet$ ; and the resolution limit perpendicular to the wavepath is denoted by $2 \Delta r$ . The resolution limits for reflection migration in e) are for poststack data, where $X$ corresponds to aperture width, and $\Delta x$ and $\Delta z$ correspond to the skinniest width and thickness of the fat migration ellipse.

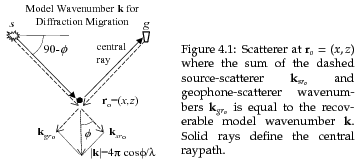
The resolution limits for migration (Berkhout, 1984; Safar, 1985; Vermeer, 1997; Chen and Schuster, 1999) were later found to be equivalent to those for linearized inversion in a homogeneous (Devaney, 1984; Wu and Toksoz, 1987) and an inhomogeneous medium (Beylkin, 1985) with smooth velocity variations. The key idea is that the model wavenumber vector ${\bf {k}}$ can be equated to the sum of the source-scatterer and geophone-scatterer wavenumbers ${\bf {k}}={\bf {k}}_{gr_o}+{\bf {k}}_{sr_o}$ shown in Figure 4.5. If ${\mathcal D}$ defines the range of wavenumbers available from the source-receiver positions, then the horizontal $\Delta x$ and vertical $\Delta z$ spatial resolution limits of the migration image are defined as

$$\Delta x = \min_{ {\mathcal D}} [ \frac{2 \pi}{k_{gx}+k_{sx}}],$$

$$\Delta z = \min_{ {\mathcal D}} [\frac{2 \pi}{k_{gz}+k_{sz}}].$$ (4.2)

In the farfield approximation these limits are given in Figure 4.4e for poststack migration.

The above resolution analysis have been developed for migration and traveltime tomography, and until now, there has not been a comprehensive treatment of the resolution limits associated with FWI. I now present such an analysis by applying an asymptotic analysis to the model resolution function for FWI. The resulting resolution formulas can be used to better understand and optimize the resolution characteristics of FWI, LSM, and RTM.

This chapter is organized into three sections. The introduction heuristically explains how wavepaths are used to estimate resolution for both traveltime tomography and migration. This leads to an intuitive description of spatial resolution as the minimum width and height of the intersection of Fresnel zones at the trial image point. The next section validates this heuristic definition by rigorously deriving the resolution limits for each type of wavepath, and explains their relationship to the acquisition geometry. Finally, a discussion and summary is given.