Migration versus successive steepest descent

Given a set of sampled Hessians (or equivalently sampled modeling operators) and the associated data generated according to an underlining model ${\bf {m}}$ , I investigate two strategies, with the knowledge of these sampled Hessians and observed data, to get an estimate of ${\bf {m}}$ : 1) migration and 2) successive steepest descent (SSD). The question I intend to address is, which strategy is better in terms of producing a more accurate estimate?

Let $\mathbf{L_1},\ldots, \mathbf{L_n}$ and $\mathbf{d_1},\ldots, \mathbf{d_n}$ respectively be the $n$ copies of sampled modeling operators and the data generated according to

$$\mathbf{d_i} = \mathbf{L_i} {\bf {m}}, ~~\forall i=1,\dots,n.$$ (9.1)

The migration strategy forms the estimate as

$${\bf {m}}_{mig} = \sum_{i=1}^{n} \mathbf{L_i}^\dagger \mathbf{d_i}.$$ (9.2)

On the other hand, the SSD strategy consists of the following steps:

1. Start from ${\bf {m}}^{(0)}_{SSD} = {\bf {0}}$ .
2. At the $k^\textrm{th}$ step, presented with $\mathbf{L_k}$ and $\mathbf{d_k}$ , update the trial model once, according to the steepest descent formula, prescribed as :

   $${\bf {m}}^{(k+1)}_{SSD} = {\bf {m}}^{(k)}_{SSD} + \alpha {\bf {g}},$$ (9.3)

   $$\noalign{where} {\bf {g}} = \mathbf{L_k}^\dagger (\mathbf{d_k} - {\bf {m}}^{(k)}_{SSD}),$$ (9.4)

   $$\alpha = \frac{\vert\vert{\bf {g}}\vert\vert^2}{\vert\vert\mathbf{L_k}{\bf {g}}\vert\vert^2}.$$ (9.5)

   
   

3. Finish at $k=n$ .

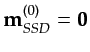To fairly evaluate the model error, I introduce

$$\theta^\epsilon({\bf {x}}) \stackrel{\mathrm{def}}{=}\measuredangle({\bf {x}},{\bf {m}}) = \arccos(\frac{{\bf {x}}^T \cdot {\bf {m}}}{\vert\vert{\bf {x}}\vert\vert ~\vert\vert{\bf {m}}\vert\vert}),$$ (9.6)

a criterion that ignores the magnitudes of the vectors in question.

Unable to establish a mathematical bound on $\theta^\epsilon({\bf {m}}_{mig})$ in comparison to $\theta^\epsilon({\bf {m}}_{SSD})$ , I resort to a Monte Carlo method instead. In this study, ${\bf {d}}\in \mathbb{R}^{10}$ and ${\bf {m}}\in \mathbb{R}^{25}$ . The sizes are deliberately chosen to make each individual inverse problem, i.e., to invert equation D.1, which is underdetermined. In addition, the performance of the two strategies in the presence of noise is probed. Specifically, a line of code

$$\mathbf{d_i} \gets \mathbf{d_i} + {\bf {r}}$$ (9.7)

follows immediately after equation D.1, and all succeeding operations are based on the noisy $\mathbf{d_i}$ 's. Here, ${\bf {r}}$ is a vector of white Gaussian noise, with its power adjusted to meet a given choice of SNR.

Figure D.1: Scatter plot of the model errors in terms of $\theta^\epsilon$ , for migration and for SSD, when (upper row) data is not contaminated by noise and (lower row) SNR=10dB, with the set size $n$ varying from (left column) 2, to (middle column) 3, and to (right column) 10. In all the panels, data points corresponding to $\theta^\epsilon({\bf{m}}_{mig}) >= \theta^\epsilon({\bf{m}}_{SSD})$ are plotted in black, while points corresponding to $\theta^\epsilon({\bf{m}}_{mig}) < \theta^\epsilon({\bf{m}}_{SSD})$ are plotted in red.

The results are summarized in Figure D.1. Here, the $\mathbf{L_i}$ 's and ${\bf {m}}$ are generated using a Gaussian distribution. I have varied the types of distribution, from Gaussian to a sparse distribution such as binomial, and qualitatively the same trends are observed: SSD produces smaller model error than migration does, except for a few rare exceptions. As the size of the random set grows (i.e., more stackings in migration and more updates in SSD), the advantage of SSD becomes even more apparent. As plotted in the upper right panel, $\theta^\epsilon({\bf {m}}_{mig}) / \theta^\epsilon({\bf {m}}_{SSD}) \approx 24/6$ . When $\mathbf{d_i}$ 's are corrupted by noise, however, the performance of SSD deteriorates more than that of migration. But at this level of noise in most cases SSD still outperforms migration.

These observations are intuitively understandable. Migration can be thought of as one step of steepest descent starting from $\bf {0}$ . Over a set of $n$ samples, migration amounts to averaging n attempts of steepest descent, each starting from $\bf {0}$ , whereas in SSD, the trial model keeps improving. So it's very probable that the latter outperforms the former. It could happen that the average of these `first attempts' comes very close to the true model. This explains why exceptions exist. In the presence of white noise, averaging with equal weight over random instances, as migration does, is the most effective means to reduce noise. In SSD, however, the earlier updates influence the iteration trajectory more than the later updates do. In effect, the end result senses a weighted average of the noise contained in each update, with larger weight assigned to early samples and smaller weight to later samples, resulting in less noise reduction than what migration is capable of.