Next: Resolution Limits for Imaging Up: Thesis Previous: Migration versus successive steepest Contents
I first analyze the resolution of the ellipse depicted in Figure 4.1b, and then relate the parameters of this ellipse to those defining a wavepath.
The spatial resolution limit near the point ![]() in Figure 4.1b is related to the reciprocal of the segment length
in Figure 4.1b is related to the reciprocal of the segment length
![]() .
This length can be determined by noting that
the end points
.
This length can be determined by noting that
the end points ![]() and
and ![]() satisfy both the equations of the ellipse and the line, written as
satisfy both the equations of the ellipse and the line, written as
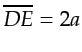 when
when 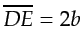 when
when
Next, the parameters ![]() and
and ![]() of the ellipse are related to those defining the first Fresnel zone, as depicted in Figure 4.1a. Let
of the ellipse are related to those defining the first Fresnel zone, as depicted in Figure 4.1a. Let ![]() and
and ![]() be the two foci of the ellipse, the distance between
be the two foci of the ellipse, the distance between ![]() and
and ![]() be
be ![]() ,
and
,
and ![]() be an arbitrary point on the ellipse.
The first Fresnel zone is delimited by points
be an arbitrary point on the ellipse.
The first Fresnel zone is delimited by points ![]() on the ellipse that satisfy
on the ellipse that satisfy
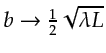 .
.
From equations E.7, E.8, and E.3, we see that
the resolution can be written as
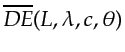 , a function of
wavepath parameters
, a function of
wavepath parameters
![]() , and intersection parameters
, and intersection parameters ![]() and
and ![]() .
.