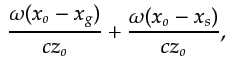Determinant of Jacobian Matrix
The transformation between the data coordinates 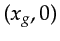 ,
, 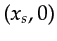 and
and
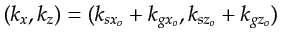 is given by
is given by
![$\displaystyle \left( \begin{array}{c} dk_x \\ dk_z \end{array} \right) = \left[...
...} \end{array} \right] \left( \begin{array}{c} dx_g \\ dx_s \end{array} \right),$](img655.png) |
(12.1) |
where the 2x2 matrix is the Jacobian matrix.
The scaled determinant 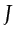 of the Jacobian matrix is
given by
of the Jacobian matrix is
given by
so that
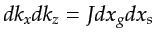 .
In the case of a homogeneous medium with velocity
.
In the case of a homogeneous medium with velocity  and a scatterer at
and a scatterer at
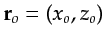 ,
the model wavenumbers are
,
the model wavenumbers are
so that the partial derivatives of the wavenumbers
can be easily determined. For a heterogeneous medium,
the derivatives can be approximated by
finite-difference approximations to the first-order derivatives
and the wavenumbers can be computed
by a ray tracing method.
Under the farfield approximation  , where
, where 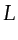 is the aperture
width of the source-geophone array, so equation G.3 becomes
is the aperture
width of the source-geophone array, so equation G.3 becomes
where the horizontal wavenumbers are now linear functions
of the data variables 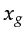 and
and 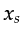 .
This means that equation F.7
represents the inverse Fourier
transform of the model spectrum.
Yunsong Huang
2013-09-22
.
This means that equation F.7
represents the inverse Fourier
transform of the model spectrum.
Yunsong Huang
2013-09-22
![]() ,
, ![]() and
and
![]() is given by
is given by