Resolution Limits for Imaging Diving Wave Residuals
The resolution limits for imaging diving wave residuals are
rigorously derived by multiplying the
migration kernel in Figure 4.4a by the expression for the diving-wave arrival
where the integral over the model-space region 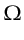 is approximated by the one over
the region
is approximated by the one over
the region
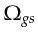 . Here,
. Here,
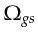 coincides with the yellow first Fresnel zone of the diving wave
in Figure 4.4a
for the source-geophone pair denoted by
coincides with the yellow first Fresnel zone of the diving wave
in Figure 4.4a
for the source-geophone pair denoted by 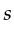 and
and  .
This approximation recognizes that only model perturbations
within the first Fresnel zone of the diving
wave will strongly affect the timing and/or amplitude of the diving-wave
arrival at
.
This approximation recognizes that only model perturbations
within the first Fresnel zone of the diving
wave will strongly affect the timing and/or amplitude of the diving-wave
arrival at 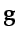 .
.
Plugging equation F.1
into equation 4.6 gives
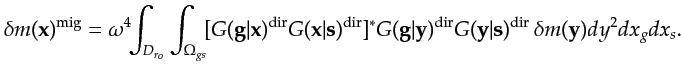 |
(11.2) |
We now assume a localized subwavelength perturbation
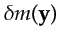 centered
at
centered
at
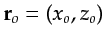 that is non-zero only within a fraction of a wavelength
from
that is non-zero only within a fraction of a wavelength
from
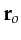 . In this case, the range of source-geophone pairs
in
. In this case, the range of source-geophone pairs
in 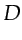 is restricted to
the set
is restricted to
the set 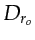 of source-geophone pairs that allow for first Fresnel diving wavepaths
to visit the localized perturbation
centered at
of source-geophone pairs that allow for first Fresnel diving wavepaths
to visit the localized perturbation
centered at
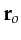 .
These
source-geophone pairs are the only ones whose transmitted diving waves11.1 will
be significantly influenced by the model perturbations centered at
.
These
source-geophone pairs are the only ones whose transmitted diving waves11.1 will
be significantly influenced by the model perturbations centered at
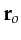 .
For example, if the image point is at
.
For example, if the image point is at 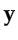 and the geophone is at
and the geophone is at 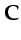 in Figure 4.6b,
then
in Figure 4.6b,
then 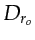 is limited to the sources between
is limited to the sources between 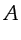 and
and 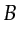 .
If the wavepaths are those for a specular reflection, then
the range of source locations in
.
If the wavepaths are those for a specular reflection, then
the range of source locations in
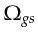 is between
is between 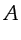 and
and 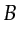 in Figure 4.6a.
in Figure 4.6a.
For a smooth background velocity
we assume the following asymptotic Green's function
for the migration and data kernels
 |
(11.3) |
so that equation F.2 becomes
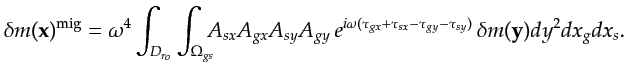 |
(11.4) |
Here, 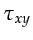 is the traveltime for the transmitted wave
to propagate from
is the traveltime for the transmitted wave
to propagate from 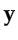 to
to  , and
, and  is its
attendant geometrical spreading term that
satisfies the transport equation.
is its
attendant geometrical spreading term that
satisfies the transport equation.
Assuming that the
subwavelength scatterer represented by
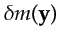 is
located within a fraction
of a wavelength from the trial image point at
is
located within a fraction
of a wavelength from the trial image point at  , then
, then  ,
, 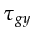 ,
,
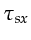 , and
, and 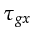 ,
can be expanded about its center point
,
can be expanded about its center point
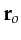 to give
to give
Inserting these approximations into equation F.4
gives
Under the far-field approximation, the geometric spreading terms can be taken outside the integral to give
![$\displaystyle \delta m({\bf {x}})^{\textrm{mig}} = \omega^4 \int_{ D_{r_o}}\!\!...
... \tau_{sr_o}) \cdot [{\bf {y}}-{\bf {x}}]} \,\delta m({\bf {y}})dy^2 dx_g dx_s.$](img630.png) |
(11.6) |
Here, the gradient of the traveltime field
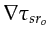 is parallel
to the direct wave's incident angle at
is parallel
to the direct wave's incident angle at
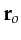 ,
so, according to the dispersion equation,
,
so, according to the dispersion equation,
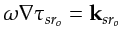 can be identified as the source-to-scatterer point wavenumber vector
can be identified as the source-to-scatterer point wavenumber vector
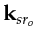 ;
similarly, the geophone-to-scatterer wavenumber is denoted as
;
similarly, the geophone-to-scatterer wavenumber is denoted as
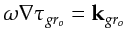 .
This means that,
by definition of the Fourier transform with a restricted domain of integration
.
This means that,
by definition of the Fourier transform with a restricted domain of integration
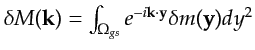 , equation F.6 becomes
, equation F.6 becomes
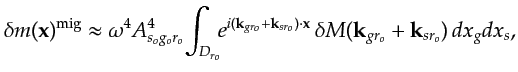 |
(11.7) |
where
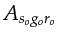 approximates
the geometrical
spreading for the scatterer
at
approximates
the geometrical
spreading for the scatterer
at
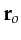 with the range of allowable source-geophone pairs centered around the pairs denoted by
with the range of allowable source-geophone pairs centered around the pairs denoted by 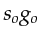 , the Fourier spectrum of the model is given by
, the Fourier spectrum of the model is given by
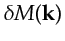 ,
and the model wavenumber components
,
and the model wavenumber components
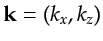 are
are
where
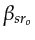 and
and
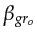 denote the
incidence angles of the source and geophone rays, respectively,
at the scatterer's location
denote the
incidence angles of the source and geophone rays, respectively,
at the scatterer's location
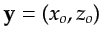 . As shown in the appendix, these
incidence angles are implicit functions of the
source
. As shown in the appendix, these
incidence angles are implicit functions of the
source 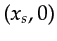 , geophone
, geophone 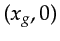 , and scatterer
, and scatterer
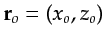 coordinates.
coordinates.
The determinant of the Jacobian in
equation G.2 (see Appendix G) can be used
to map the 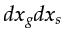 integration in equation F.7
to a
integration in equation F.7
to a 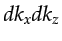 integration:
integration:
where
 is the set of wavenumbers that equation F.8 maps from the source-geophone pairs in
is the set of wavenumbers that equation F.8 maps from the source-geophone pairs in 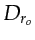 for the scatterer at
for the scatterer at
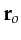 , and
, and
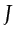 is the determinant of the
Jacobian matrix in
equation G.2.
Yunsong Huang
2013-09-22
is the determinant of the
Jacobian matrix in
equation G.2.
Yunsong Huang
2013-09-22
![]() is
located within a fraction
of a wavelength from the trial image point at
is
located within a fraction
of a wavelength from the trial image point at ![]() , then
, then ![]() ,
, ![]() ,
,
![]() , and
, and ![]() ,
can be expanded about its center point
,
can be expanded about its center point
![]() to give
to give
![$\displaystyle \delta m({\bf {x}})^{\textrm{mig}} \approx \omega^4 \int_{D_{r_o}...
... \tau_{sr_o}) \cdot [{\bf {y}}-{\bf {x}}]} \,\delta m({\bf {y}})dy^2 dx_g dx_s.$](img629.png)
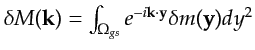 , equation F.6 becomes
, equation F.6 becomes
![]() integration in equation F.7
to a
integration in equation F.7
to a ![]() integration:
integration: