Least-squares Phase-encoded GDM

The LSM method can be applied to the phase-encoded multisource data by a steepest descent method:

$$\bf {m}^{(k+1)} = \bf {m}^{(k)} - \alpha \bf {L}^T [\bf {L}\bf {m}^{(k)} - \bf {d}],$$ (24)

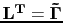where $\alpha$ is the step length, $\bf {L}^T=\tilde{\Gamma}$ is the multisource migration operator with the kernel given by equation . The key idea is to solve the wave equation only once to get the Green’s functions. The multisource migration operator is obtained by convolution of the receiver-side Green's function and source-side Green's function followed by phase-encoding and then saved on disk. For each LSM iteration, the saved multisource migration kernels are loaded and zero-lag cross-correlated with the data residuals obtained from the previous iteration.