



Next: Compression of the Migration
Up: Generalized Diffraction-Stack Migration
Previous: Summary
Contents
Computation of the Migration Kernel
The migration kernel in equation ![[*]](crossref.png) can be computed
in one of two ways.
can be computed
in one of two ways.
- Place a source point on the surface at
 , and solve for the field everywhere
in the model
by a finite-difference method to get the Green's function
, and solve for the field everywhere
in the model
by a finite-difference method to get the Green's function
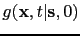 . Reciprocity says that
. Reciprocity says that
 , and if we replace
, and if we replace
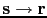 then this gives
then this gives
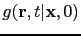 .
Thus,
.
Thus,
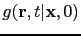 can be convolved with
can be convolved with
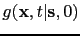 to give the
migration kernel
to give the
migration kernel
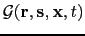 in equation
in equation ![[*]](crossref.png) with the receiver at
with the receiver at 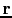 and the source at
and the source at  for all subsurface points
for all subsurface points 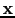 .
.
- Alternatively, a point source
can be placed at depth
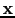 and the field
can be solved everywhere
to get
and the field
can be solved everywhere
to get
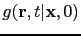 . This can be cost effective
for target-oriented migration (or waveform inversion)
so that we only
need the Green's functions for point sources along
the boundary
of the target (Dong et al., 2009). Reciprocity says that
. This can be cost effective
for target-oriented migration (or waveform inversion)
so that we only
need the Green's functions for point sources along
the boundary
of the target (Dong et al., 2009). Reciprocity says that
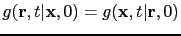 ,
and letting
,
and letting
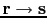 yields
yields
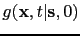 .
The migration kernel at
.
The migration kernel at 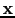 can now be computed by equation
can now be computed by equation ![[*]](crossref.png) . This is the method used by
Liu and Wang (2008) and Dong et al. (2009)
for target-oriented migration.
. This is the method used by
Liu and Wang (2008) and Dong et al. (2009)
for target-oriented migration.
Zhou and Schuster (2002)
demonstrated how to efficiently compute these
migration operators by finite differencing along the leading
portion of the wavefront.




Next: Compression of the Migration
Up: Generalized Diffraction-Stack Migration
Previous: Summary
Contents
Ge Zhan
2013-07-08
![[*]](crossref.png) with the receiver at
with the receiver at ![[*]](crossref.png) . This is the method used by
Liu and Wang (2008) and Dong et al. (2009)
for target-oriented migration.
. This is the method used by
Liu and Wang (2008) and Dong et al. (2009)
for target-oriented migration.
![[*]](crossref.png) can be computed
in one of two ways.
can be computed
in one of two ways.
![[*]](crossref.png) with the receiver at
with the receiver at ![[*]](crossref.png) . This is the method used by
Liu and Wang (2008) and Dong et al. (2009)
for target-oriented migration.
. This is the method used by
Liu and Wang (2008) and Dong et al. (2009)
for target-oriented migration.