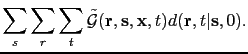


Next: Bibliography
Up: Generalized Diffraction-Stack Migration
Previous: Computation of the Migration
Contents
Compression of the Migration Kernel
A wavelet transform with compression (Zhan and Schuster, 2010)
can be used to reduce storage costs associated with the the GDM kernel, as follows.
- Compute the source-side
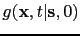 and the receiver-side
and the receiver-side
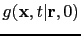 bandlimited Green's functions by a numerical solution to the wave equation.
bandlimited Green's functions by a numerical solution to the wave equation.
- A wavelet transform (Luo and Schuster, 1992) is applied to
the Green's function
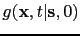 and
and
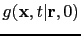 to get
to get
![$ {\mathcal W}[g({\bf {x}},t\vert{\bf {s}},0)]$](img220.png) and
and
![$ {\mathcal W}[g({\bf {x}},t\vert{\bf {r}},0)]$](img221.png) , respectively.
Here,
, respectively.
Here,
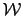 represents the
wavelet transform with up to an order-of-magnitude
reduction in storage requirements (Luo and Schuster, 1992). Then, mute all wavelet coefficients
below a given threshold in the wavelet domain and only store the significant coefficients to get the compressed
Green's functions
represents the
wavelet transform with up to an order-of-magnitude
reduction in storage requirements (Luo and Schuster, 1992). Then, mute all wavelet coefficients
below a given threshold in the wavelet domain and only store the significant coefficients to get the compressed
Green's functions
![$ {\mathcal W}[\tilde{g}({\bf {x}},t\vert{\bf {s}},0)]$](img223.png) and
and
![$ {\mathcal W}[\tilde{g}({\bf {x}},t\vert{\bf {r}},0)]$](img224.png) . Save these compressed
Green's functions on the disk.
. Save these compressed
Green's functions on the disk.
- After reading these compressed Green's functions from disk, an inverse wavelet transform is performed to
reconstruct the Green's functions
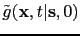 and
and
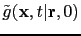 by decompressing
by decompressing
![$ {\mathcal W}[\tilde{g}({\bf {x}},t\vert{\bf {s}},0)]$](img223.png) and
and
![$ {\mathcal W}[\tilde{g}({\bf {x}},t\vert{\bf {r}},0)]$](img224.png) .
This is
followed by a convolution step using a FFT to get the compressed migration kernel
.
This is
followed by a convolution step using a FFT to get the compressed migration kernel
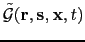 in equation
in equation ![[*]](crossref.png) :
:
where
![$ \tilde{g}({\bf {x}},t\vert{\bf {r}},0) = {\mathcal W}^{-1} [\tilde g({\bf {x}},t\vert{\bf {r}},0)]$](img228.png) .
Here, tilde denotes the function after lossy compression and decompression.
.
Here, tilde denotes the function after lossy compression and decompression.
- The compressed migration operator
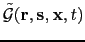 is a Kirchhoff-like kernel
that describes, for a single shot gather, pseudo-hyperbolas of multiarrivals in
is a Kirchhoff-like kernel
that describes, for a single shot gather, pseudo-hyperbolas of multiarrivals in  -
-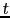 coordinates.
The reflection energy in a recorded shot gather
coordinates.
The reflection energy in a recorded shot gather
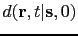 is then summed along such pseudo-hyperbolas to
give the migration image,
is then summed along such pseudo-hyperbolas to
give the migration image,
This summation is equivalent to a dot product between the recorded shot gathers and the compressed GDM kernels,
and has the advantage over
Kirchhoff migration in that there is no high-frequency approximation and multiarrivals
are included in the imaging.



Next: Bibliography
Up: Generalized Diffraction-Stack Migration
Previous: Computation of the Migration
Contents
Ge Zhan
2013-07-08
![[*]](crossref.png) :
: