Hybrid pseudospectral/finite-difference scheme

For every time step, the TTI pure P-wave computation in equation 4.10 requires two forward FFTs and twelve inverse FFTs, which are computationally intensive. By revisiting equation 4.9, I find that due to the appearance of the wavenumbers in the denominators, equation 4.9c must be evaluated using the pseudospectral method and it would be difficult to derive pure finite-difference operators that correspond to the six right-hand-side terms. However, there are no such terms in equations 4.9a and 4.9b. To greatly reduce the computation time while avoiding spurious shear-wave artifacts as well as numerical instabilities, I propose a hybrid pseudospectral/finite-difference scheme to evaluate the TTI pure P-wave equation in equation 4.10. That is, transforming equations 4.9a and 4.9b using the relations 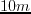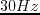$k_x \leftrightarrow -i\frac{\partial}{\partial x}$ , $k_y \leftrightarrow -i\frac{\partial}{\partial y}$ , yields

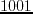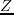where $V'$ and $H'$ can be approximated by finite-difference operators applied along the symmetry axis and symmetry plane, respectively. Spatial derivatives in the above equation can be cheaply computed using a second, fourth or higher order finite-difference scheme instead of using FFTs back and forth.

Although wavenumber terms in equation 4.9c can not all be replaced by corresponding finite-difference operators, it could be partially approximated as follows

Notice that the number of wavenumber terms in equation 4.11c is reduced from six to three. And 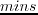$T'$ can now be approximated by finite-difference operators as well as 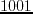$V'$ and $H'$ .

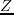Therefore, the resulting hybrid solution to the TTI pure P-wave equation becomes

$$u(\vecx ,t+\dt ) = 2u(\vecx ,t) - u(\vecx ,t-\dt ) - \dt ^2 \bigg[ v_v^2V' + v_h^2H' + (v_n^2-v_h^2)T' \bigg] u(\vecx ,t).$$ (412)

Noticeably, this new proposed hybrid strategy only requires four (one forward and three inverse) 3D FFTs per time step in simulating a pure P-wave propagation in a 3D TTI medium. For a 2D model, the number of FFTs reduces to three per time step in the hybrid method.