


Next: Hybrid pseudospectral/finite-difference scheme
Up: Numerical Implementations
Previous: Numerical Implementations
Contents
The pseudospectral method is proposed by Kosloff and Baysal (1982),
which uses Fourier transformation, multiplication by 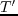 in the wavenumber domain,
and inverse Fourier transformation back to the spatial domain
to compute the spatial derivatives.
Differential operators
in the wavenumber domain,
and inverse Fourier transformation back to the spatial domain
to compute the spatial derivatives.
Differential operators 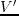 ,
, 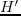 and
and 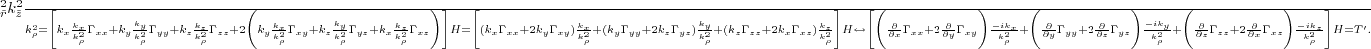 in equation 4.9 are written
in the wavenumber domain
and are easily evaluated there with a pseudospectral method.
Meanwhile, as in the pseudospectral method,
performing the operations in the wavenumber domain
guarantees that it will not suffer from numerical dispersion.
in equation 4.9 are written
in the wavenumber domain
and are easily evaluated there with a pseudospectral method.
Meanwhile, as in the pseudospectral method,
performing the operations in the wavenumber domain
guarantees that it will not suffer from numerical dispersion.
Substituting equations 4.5 and 4.9 into equation 4.2,
I write the TTI pure P-wave equation as
![$\displaystyle u(\vecx ,t+\dt ) = 2u(\vecx ,t) - u(\vecx ,t-\dt )
- \dt ^2 \bigg[ v_v^2V + v_h^2H + (v_n^2-v_h^2)T \bigg] u(\vecx ,t).$](img124.png) |
(410) |
From the above equations, we can see that at each time step of a 3D simulation, the
evaluation of the differential operator 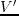 demands at least a 3D forward FFT of the wavefield
plus six 3D inverse FFTs. A similar analysis applies to the differential operator
demands at least a 3D forward FFT of the wavefield
plus six 3D inverse FFTs. A similar analysis applies to the differential operator  as well.
Therefore, a total of fourteen 3D FFTs are required to simulate the pure P-wave wavefield at each time step in a TTI medium.
When it comes to 2D, all
as well.
Therefore, a total of fourteen 3D FFTs are required to simulate the pure P-wave wavefield at each time step in a TTI medium.
When it comes to 2D, all 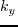 terms are eliminated, and thus only eight 2D FFTs are needed.
terms are eliminated, and thus only eight 2D FFTs are needed.



Next: Hybrid pseudospectral/finite-difference scheme
Up: Numerical Implementations
Previous: Numerical Implementations
Contents
Ge Zhan
2013-07-09
![$\displaystyle u(\vecx ,t+\dt ) = 2u(\vecx ,t) - u(\vecx ,t-\dt )
- \dt ^2 \bigg[ v_v^2V + v_h^2H + (v_n^2-v_h^2)T \bigg] u(\vecx ,t).$](img124.png)
![]() demands at least a 3D forward FFT of the wavefield
plus six 3D inverse FFTs. A similar analysis applies to the differential operator
demands at least a 3D forward FFT of the wavefield
plus six 3D inverse FFTs. A similar analysis applies to the differential operator ![]() as well.
Therefore, a total of fourteen 3D FFTs are required to simulate the pure P-wave wavefield at each time step in a TTI medium.
When it comes to 2D, all
as well.
Therefore, a total of fourteen 3D FFTs are required to simulate the pure P-wave wavefield at each time step in a TTI medium.
When it comes to 2D, all ![]() terms are eliminated, and thus only eight 2D FFTs are needed.
terms are eliminated, and thus only eight 2D FFTs are needed.