Numerical Scheme: Quasi-linear Inversion

The goal is to find a slowness perturbation $\textbf{m}(\textbf{x})$ to fit the input data 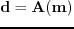$\textbf{d}=\textbf{A}(\textbf{m})$ in terms of minimizing the misfit functional

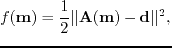$$f(\textbf{m})=\frac{1}{2}\vert\vert\textbf{A}(\textbf{m})-\textbf{d}\vert\vert^{2},$$ (29)

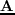where $\textbf{A}$ represents a non-linear forward modeling operator and 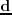$\textbf{d}$ is the input data. The iterative steepest descent solution is

$$\textbf{m}^{(k+1)}=\textbf{m}^{(k)}-\alpha \textbf{L}^{T}[\textbf{A}(\textbf{m}^{(k)})-\textbf{d}],$$ (210)

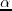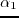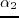where $\textbf{L}^{T}$ is the reverse time migration operator. The step length $\alpha$ is calculated with a quadratic line search method. As illustrated in Figure 2.1, two trial step lengths $\alpha_{1}$ and $\alpha_{2}$ along with the current model are used to approximate a quadratic curve. Then, the minimum point of the quadratic function is found to give the optimal step length. For simplicity, the steepest descent method is employed in equation (2.10), but in the numerical examples the preconditioned conjugate gradient method is used.

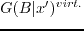Equation (2.10) represents a quasi-linear inversion method that is similar to full waveform inversion. The difference is that in equation (2.10), the migration operator $\textbf{L}^{T}$ only depends on the background slowness model $\textbf{s}_{o}$ and does not change with iterations, as the background slowness model is assumed to be accurate enough.