



Next: Forward Modeling of a
Up: Theory
Previous: Theory
Contents
Following Nihei and Li (2006) and Sirgue et al. (2008), the single frequency response of a velocity model
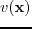 for a shot at
for a shot at
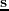 can be modelled with the time-domain finite-difference method by solving the equation
can be modelled with the time-domain finite-difference method by solving the equation
![$\displaystyle (\bigtriangledown^{2}-\frac{1}{v^2}\frac{\partial^2}{\partial t^2...
...x},\textbf{s})=-Re[W(\omega_{s})e^{i\omega_{s}t}]\delta(\textbf{x}-\textbf{s}),$](img142.png) |
(35) |
where the source wavelet is a harmonic wave with its amplitude and phase specified by the source
 .
Assuming that the trace length
.
Assuming that the trace length 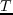 is long enough to include all the dominant arrivals, the recorded wavefield at the receiver location
is long enough to include all the dominant arrivals, the recorded wavefield at the receiver location
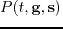 reaches steady state after propagation time
reaches steady state after propagation time 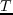 . Therefore, the single frequency response can be extracted with the following formula
. Therefore, the single frequency response can be extracted with the following formula
 |
(36) |
Note that the simulation time is increased from 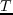 to
to 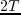 . For a single shot, the above integration can be computed over a single period (
. For a single shot, the above integration can be computed over a single period (
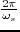 ) instead of
) instead of 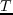 . Repeating the above solution for different frequencies and digitizing the records give the frequency domain data
. Repeating the above solution for different frequencies and digitizing the records give the frequency domain data
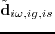 .
.




Next: Forward Modeling of a
Up: Theory
Previous: Theory
Contents
Wei Dai
2013-07-10
![$\displaystyle (\bigtriangledown^{2}-\frac{1}{v^2}\frac{\partial^2}{\partial t^2...
...x},\textbf{s})=-Re[W(\omega_{s})e^{i\omega_{s}t}]\delta(\textbf{x}-\textbf{s}),$](img142.png)