



Next: Single Frequency Response Modeling
Up: Least-squares Reverse Time Migration
Previous: Introduction
Contents
A time-domain seismic dataset
 , where
, where
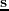 and
and
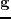 are source and receiver vectors, can be digitized into a 3D array
are source and receiver vectors, can be digitized into a 3D array
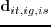 (
(
 ), assuming there are
), assuming there are 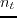 time samples,
time samples, 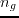 receivers for a shot, and
receivers for a shot, and 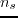 shots in total.
Given time sampling
shots in total.
Given time sampling 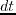 , the time domain array can be transformed to the frequency domain as
, the time domain array can be transformed to the frequency domain as
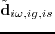 (
(
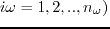 and the angular frequency sampling is
and the angular frequency sampling is
 .
In the frequency domain, only these samples that fall into the frequency band of the seismic data are kept, so for a dataset with peak frequency
.
In the frequency domain, only these samples that fall into the frequency band of the seismic data are kept, so for a dataset with peak frequency 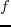 (frequency band
(frequency band
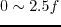 ),
),
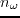 can be calculated as
can be calculated as
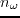 =
=
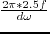 .
.
With the frequency-selection encoding, the encoding function is defined as
 |
(31) |
where  is a function of shot index
is a function of shot index 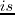 , and it represents the selected frequency for the shot.
Similar to conventional blended source technique, all the shots are encoded with the encoding function and blended together to form a supergather
, and it represents the selected frequency for the shot.
Similar to conventional blended source technique, all the shots are encoded with the encoding function and blended together to form a supergather
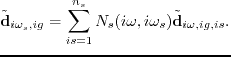 |
(32) |
Now the supergather
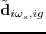 becomes a 2D array, and each frequency component corresponds to a different shot. Note that a supergather can only accommondate up to
becomes a 2D array, and each frequency component corresponds to a different shot. Note that a supergather can only accommondate up to
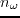 shots.
It is obvious that the frequency-selection encoding method is applicable to seismic data with a marine streamer acquisition geometry, because at each receiver position, the data components from different shots can be distinguished from one another according to their frequency contents.
shots.
It is obvious that the frequency-selection encoding method is applicable to seismic data with a marine streamer acquisition geometry, because at each receiver position, the data components from different shots can be distinguished from one another according to their frequency contents.
In least-squares reverse time migration, a reflectivity model vector
 is sought to best fit the observed data with a Born modeling operator
is sought to best fit the observed data with a Born modeling operator
 by minimizing the misfit functional
by minimizing the misfit functional
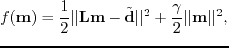 |
(33) |
where
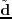 is a vector representing a supergather
is a vector representing a supergather
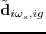 and
and 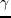 is damping coefficient.
is damping coefficient.
The following numerical scheme can be implemented with Born modeling and the reverse time migration method:
At each iteration, a new supergather with new encoding functions should be used to sample a different frequency for each shot.
Therefore, if
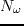 frequencies are needed to avoid wrap-around effects, the LSM procedure should be iterated at least
frequencies are needed to avoid wrap-around effects, the LSM procedure should be iterated at least
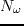 iterations to ensure that all the frequencies are visited by a shot. In contrast, the iterative stacking method can be applied to those
iterations to ensure that all the frequencies are visited by a shot. In contrast, the iterative stacking method can be applied to those
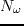 supergathers to produce an image with less computational cost than conventional RTM, because usually
supergathers to produce an image with less computational cost than conventional RTM, because usually
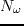 can be much smaller than
can be much smaller than
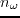 due to data reduntancy in the frequecy domain (Mulder and Plessix, 2004b).
due to data reduntancy in the frequecy domain (Mulder and Plessix, 2004b).
In the following section, I demonstrate the numerical implementation of modeling and migration of a supergather with a time-domain finite-difference method.
Subsections




Next: Single Frequency Response Modeling
Up: Least-squares Reverse Time Migration
Previous: Introduction
Contents
Wei Dai
2013-07-10
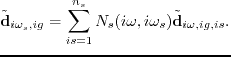
![]() is sought to best fit the observed data with a Born modeling operator
is sought to best fit the observed data with a Born modeling operator
![]() by minimizing the misfit functional
by minimizing the misfit functional